题目内容
已知函数f(x)=2x+a•2-x(a∈R).
(1)讨论函数f(x)的奇偶性;
(2)若函数f(x)在(-∞,2]上为减函数,求a的取值范围.
(1)讨论函数f(x)的奇偶性;
(2)若函数f(x)在(-∞,2]上为减函数,求a的取值范围.
考点:函数奇偶性的性质,函数单调性的性质
专题:函数的性质及应用
分析:(1)分类讨论:由奇偶性的定义分函数为奇函数和偶函数可得a值,进而可得结论;(2)由减函数可得对任意的x1<x2≤2,都有f(x1)-f(x2)>0,变形可得2x1•2x2<a恒成立,又可得(2x1•2x2)max<16,可得a≥16.
解答:
解:(1)∵f(x)=2x+a•2-x,
∴f(-x)=2-x+a•2x,
若f(x)为偶函数,则对任意的x∈R,都有f(x)=f(-x),
即2x+a•2-x=2-x+a•2x对任意的x∈R都成立.
化简可得(2x-2-x)(1-a)=0对任意的x∈R都成立.
由于2x-2-x不恒等于0,故有1-a=0,即a=1
∴当a=1时,f(x)是偶函数;
若f(x)为奇函数,则对任意的x∈R,都有f(x)=-f(-x),
即2x+a•2-x+2-x+a•2x=0,(2x+2-x)(1+a)=0对任意的x∈R都成立.
由于2x+2-x不恒等于0,故有1+a=0,即a=-1
∴当a=-1时,f(x)是奇函数,
综上可得当a=1时,f(x)是偶函数;
当a=-1时,f(x)是奇函数;
当a≠±1时,f(x)是非奇非偶函数.
(2)∵函数f(x)在(-∞,2]上为减函数,
∴对任意的x1<x2≤2,都有f(x1)-f(x2)>0,
即f(x1)-f(x2)=(2x1-2x2)(1-
)>0恒成立.
由2x1-2x2<0,知1-
<0恒成立,即2x1•2x2<a恒成立.
由于当x1<x2≤2时(2x1•2x2)max<16,
∴a≥16
∴f(-x)=2-x+a•2x,
若f(x)为偶函数,则对任意的x∈R,都有f(x)=f(-x),
即2x+a•2-x=2-x+a•2x对任意的x∈R都成立.
化简可得(2x-2-x)(1-a)=0对任意的x∈R都成立.
由于2x-2-x不恒等于0,故有1-a=0,即a=1
∴当a=1时,f(x)是偶函数;
若f(x)为奇函数,则对任意的x∈R,都有f(x)=-f(-x),
即2x+a•2-x+2-x+a•2x=0,(2x+2-x)(1+a)=0对任意的x∈R都成立.
由于2x+2-x不恒等于0,故有1+a=0,即a=-1
∴当a=-1时,f(x)是奇函数,
综上可得当a=1时,f(x)是偶函数;
当a=-1时,f(x)是奇函数;
当a≠±1时,f(x)是非奇非偶函数.
(2)∵函数f(x)在(-∞,2]上为减函数,
∴对任意的x1<x2≤2,都有f(x1)-f(x2)>0,
即f(x1)-f(x2)=(2x1-2x2)(1-
| a |
| 2x12x2 |
由2x1-2x2<0,知1-
| a |
| 2x12x2 |
由于当x1<x2≤2时(2x1•2x2)max<16,
∴a≥16
点评:本题考查函数的奇偶性和单调性,涉及分类讨论的思想,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数是偶函数,且在[0,1]上单调递增的是( )
A、y=cos(x+
| ||
| B、y=1-2cos22x | ||
| C、y=-x2 | ||
| D、y=|sin(π+x)| |
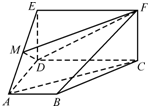 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=