题目内容
在平面直角坐标系xOy中,圆C的方程为x2+y2+8x+15=0,若直线y=kx上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围是 .
考点:圆的一般方程
专题:直线与圆
分析:由题意可得,圆心C(-4,0)到直线y=kx的距离d小于或等于半径加1,即
≤2,由此求得k的范围.
| |-4k-0| | ||
|
解答:
解:圆C的方程为x2+y2+8x+15=0,整理得:(x+4)2+y2=1,
表示圆C是以(-4,0)为圆心,1为半径.
又直线y=kx上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
则圆心C(-4,0)到直线y=kx的距离d小于或等于半径加1,
即
≤2,解得
≤k≤
,
故答案为:[-
,
].
表示圆C是以(-4,0)为圆心,1为半径.
又直线y=kx上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
则圆心C(-4,0)到直线y=kx的距离d小于或等于半径加1,
即
| |-4k-0| | ||
|
| ||
| 3 |
| ||
| 3 |
故答案为:[-
| 4 |
| 3 |
| ||
| 3 |
点评:本题主要考查直线和圆的位置关系的应用,点到直线的距离公式,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
阅读如图的程序框图,运行相应的程序,则输出S的值为( )


| A、2013×1006 |
| B、2013×1007 |
| C、2015×1007 |
| D、2015×1008 |
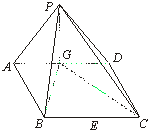 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.