题目内容
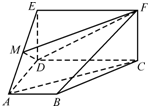 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=| 1 |
| 2 |
(Ⅰ)试确定点M的位置,使AC∥平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)首先,根据所给图形,得到当M是线段AE的中点时,AC∥平面MDF.然后,根据线面平行的判定定理进行证明即可;
(Ⅱ)利用补图法,将几何体ADE-BCF补成三棱柱ADE-B′CF,然后,借助于柱体和椎体的体积公式进行求解即可.
(Ⅱ)利用补图法,将几何体ADE-BCF补成三棱柱ADE-B′CF,然后,借助于柱体和椎体的体积公式进行求解即可.
解答:
解析:(Ⅰ)当M是线段AE的中点时,AC∥平面MDF.证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,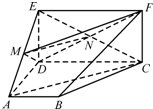
由于MN?平面MDF,又AC?平面MDF,
所以AC∥平面MDF.
(Ⅱ)如图,将几何体ADE-BCF补成三棱柱ADE-B′CF,
三棱柱ADE-B′CF的体积为V=S△ADE•CD=
×2×2×4=8,
则几何体ADE-BCF的体积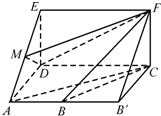 VADE-BCF=V三棱柱ADE-BCF-VF-BB'C=8-
VADE-BCF=V三棱柱ADE-BCF-VF-BB'C=8-
×(
×2×2)×2=
.
三棱锥F-DEM的体积V三棱锥M-DEF=
×(
×2×4)×1=
,
故两部分的体积之比为
:(
-
)=
(答1:4,4,4:1均可).
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,

由于MN?平面MDF,又AC?平面MDF,
所以AC∥平面MDF.
(Ⅱ)如图,将几何体ADE-BCF补成三棱柱ADE-B′CF,
三棱柱ADE-B′CF的体积为V=S△ADE•CD=
| 1 |
| 2 |
则几何体ADE-BCF的体积
 VADE-BCF=V三棱柱ADE-BCF-VF-BB'C=8-
VADE-BCF=V三棱柱ADE-BCF-VF-BB'C=8-| 1 |
| 3 |
| 1 |
| 2 |
| 20 |
| 3 |
三棱锥F-DEM的体积V三棱锥M-DEF=
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
故两部分的体积之比为
| 4 |
| 3 |
| 20 |
| 3 |
| 4 |
| 3 |
| 1 |
| 4 |
点评:本题综合考查了线面平行的判定定理、柱体和椎体的体积公式等知识,属于中档题,在解题中,如果求解不规则几何体的体积时,一般用割补法进行运算和求解,这就是转化思想在解题中的应用.

练习册系列答案
相关题目
设P(2,3),动点Q(x,y)的坐标x,y满足约束条件:
,则|
|cos∠POQ的最小值为( )
|
| OQ |
A、
| ||||
B、
| ||||
| C、7 | ||||
D、
|