题目内容
15.若点P(x,y)在曲线$\left\{{\begin{array}{l}{x=-1+cosθ}\\{y=sinθ}\end{array}}\right.$(θ为参数,θ∈R)上,则$\frac{y}{x-1}$的取值范围是[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$].分析 求出曲线的参数方程,则$\frac{y}{x-1}$表示去上的点与(1,0)连线的斜率.求出过点(1,0)的曲线的切线斜率即为$\frac{y}{x-1}$的最值.
解答 解:曲线的普通方程为(x+1)2+y2=1,
过点A(1,0)作圆(x+1)2+y2=1的切线,设切线的斜率为k,
则切线方程为y=kx-k,即kx-y-k=0.
∴圆心(-1,0)到切线的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$=1,解得k=$±\frac{\sqrt{3}}{3}$.
∵P在圆上,∴-$\frac{\sqrt{3}}{3}$≤kPA≤$\frac{\sqrt{3}}{3}$.即-$\frac{\sqrt{3}}{3}$≤$\frac{y}{x-1}$≤$\frac{\sqrt{3}}{3}$.
故答案为:$[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$.
点评 本题考查了参数方程与普通方程的转化,

练习册系列答案
相关题目
5.设x∈R,若函数f(x)=ex-ln2,则f′(0)=( )
| A. | -ln2 | B. | 1-ln2 | C. | 4 | D. | 1 |
6.已知全集U=R,A={x|x>1},B={x|x<0},则集合(∁UA)∩(∁UB)=( )
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {x|0<x<1} | D. | {x|0≤x≤1} |
3.已知向量$\overrightarrow{a}$=(3,-2,1),$\overrightarrow{b}$=(-2,4,0),则4$\overrightarrow{a}$+2$\overrightarrow{b}$等于( )
| A. | (16,0,4) | B. | (8,0,4) | C. | (8,16,4) | D. | (8,-16,4) |
20.由2个人在一座8层大楼的底层进入电梯,假设每一个人自第二层开始在每一层离开电梯是等可能的,则这两个人在不同层离开电梯的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{6}{7}$ | C. | $\frac{5}{6}$ | D. | $\frac{36}{49}$ |
7.已知sin(α+β)=$\frac{1}{2},sin(α-β)=\frac{1}{10}$,则tanαcotβ=( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
5.函数g(x)=ax3+2x2+3ax在区间(-∞,$\frac{a}{3}$)内单凋递减,则a的取值范围是( )
| A. | (-∞,0] | B. | [$-\frac{2}{3}$,$\frac{2}{3}$] | C. | (-∞,-$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$) |
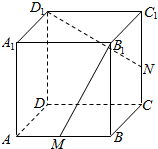 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题: