题目内容
5.函数g(x)=ax3+2x2+3ax在区间(-∞,$\frac{a}{3}$)内单凋递减,则a的取值范围是( )| A. | (-∞,0] | B. | [$-\frac{2}{3}$,$\frac{2}{3}$] | C. | (-∞,-$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$) |
分析 求导数得到g′(x)=3ax2+4x+3a,根据题意便有g′(x)≤0在($-∞,\frac{a}{3}$)上恒成立,从而得出a≤0,可看出a=0满足题意,而a<0时,可设g′(x)与x轴的左右两交点为A(x1,0),B(x2,0),从而得到${x}_{1}+{x}_{2}=-\frac{4}{3a},{x}_{1}{x}_{2}=1$,这样即可解出${x}_{1}=-\frac{2}{3a}-\sqrt{\frac{4}{9{a}^{2}}-1}$,根据题意有$\frac{a}{3}≤{x}_{1}$,这样便可得出a<0,合并a=0即可得出a的取值范围.
解答 解:g′(x)=3ax2+4x+3a;
∵g(x)在$(-∞,\frac{a}{3})$内单调递减;
∴g′(x)≤0在($-∞,\frac{a}{3}$)上恒成立;
①a=0时,显然满足题意;
②a>0时,显然不满足题意;
③a<0时,设g′(x)与x轴的左右两交点为A(x1,0),B(x2,0),则:
${x}_{1}+{x}_{2}=-\frac{4}{3a},{x}_{1}{x}_{2}=1$;
∴x1,x2均为正数,若使函数g(x)=ax3+2x2+3ax在区间(-∞,$\frac{a}{3}$)内单凋递减,
∴只需$g′(\frac{a}{3})=\frac{{a}^{3}}{3}+\frac{13}{3}a=a(\frac{{a}^{2}}{3}+\frac{13}{3})<0$
∴a<0;
∴综上得,a的取值范围为(-∞,0].
故选:A.
点评 考查函数导数符号和函数单调性的关系,韦达定理,以及一元二次方程的求根公式,无理不等式的解法,要熟悉二次函数的图象.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是(以下k∈Z)( )
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π] | B. | [kπ-$\frac{3}{8}$π,kπ+$\frac{π}{8}$] | C. | [2kπ+$\frac{π}{8}$,2kπ+$\frac{5}{8}$π] | D. | [2kπ-$\frac{3}{8}$π,2kπ+$\frac{π}{8}$] |
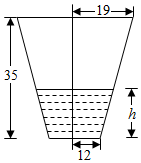 降水量是指水平地面上单位面积的降水的深度,用上口直径为38cm,底面直径为24cm,深为35cm的圆台形水桶(轴截面如图)来测量降水量,如果在一次降雨过程中,用此桶盛得的雨水正好是桶深的$\frac{1}{7}$,求这次降雨的降水量(精确到1mm).
降水量是指水平地面上单位面积的降水的深度,用上口直径为38cm,底面直径为24cm,深为35cm的圆台形水桶(轴截面如图)来测量降水量,如果在一次降雨过程中,用此桶盛得的雨水正好是桶深的$\frac{1}{7}$,求这次降雨的降水量(精确到1mm).