题目内容
20.由2个人在一座8层大楼的底层进入电梯,假设每一个人自第二层开始在每一层离开电梯是等可能的,则这两个人在不同层离开电梯的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{6}{7}$ | C. | $\frac{5}{6}$ | D. | $\frac{36}{49}$ |
分析 求出两人在同一层离开电梯的概率,则在不同层离开电梯的概率为1减去两人在同一层离开电梯的概率.
解答 解:由于每一个人自第二层开始在每一层离开电梯是等可能的,
故两人离开电梯的所有可能情况有${{A}_{7}^{1}A}_{7}^{1}$=49.
而两人在同一层离开电梯的可能情况有${C}_{7}^{1}$=7.
∴两人在同一层离开电梯的概率为$\frac{7}{49}=\frac{1}{7}$.
∴两人在不同层离开电梯的概率为1-$\frac{1}{7}=\frac{6}{7}$.
故选:B.
点评 本题考查了古典概型的概率计算,排列组合数公式的应用,属于基础题.

练习册系列答案
相关题目
11.函数$y=2sin(x+\frac{π}{3})$的图象的一个对称中心是( )
| A. | (0,0) | B. | $(-\frac{π}{3},0)$ | C. | $(\frac{π}{3},0)$ | D. | $(\frac{π}{6},0)$ |
5.在正方形ABCD之内随机选取一点M到点D的距离小于正方形的边长的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
12.已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数( )
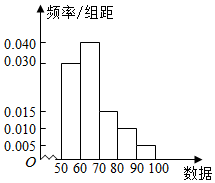

| A. | 63、64、66 | B. | 65、65、67 | C. | 65、64、66 | D. | 64、65、64 |
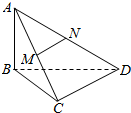 如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.