题目内容
7.已知sin(α+β)=$\frac{1}{2},sin(α-β)=\frac{1}{10}$,则tanαcotβ=( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
分析 由题意及和差角的三角函数公式整体可解得sinαcosβ和cosαsinβ的值,要求的式子切化弦,整体代入可得.
解答 解:∵sin(α+β)=$\frac{1}{2},sin(α-β)=\frac{1}{10}$,
∴sin(α+β)=sinαcosβ+cosαsinβ=$\frac{1}{2}$,
sin(α-β)=sinαcosβ-cosαsinβ=$\frac{1}{10}$,
联立以上两式可解得sinαcosβ=$\frac{3}{10}$,cosαsinβ=$\frac{1}{5}$,
∴tanαcotβ=$\frac{sinα}{cosα}$•$\frac{cosβ}{sinβ}$=$\frac{sinαcosβ}{cosαsinβ}$=$\frac{3}{2}$,
故选:A.
点评 本题考查两角和与差的三角函数公式,整体法是解决问题的关键,属基础题.

练习册系列答案
相关题目
2.△ABC的三边a,b,c成等差数列,则角B的范围是( )
| A. | $({0,\frac{π}{3}}]$ | B. | $[{\frac{π}{6},\frac{π}{2}})$ | C. | $[{\frac{π}{4},\frac{π}{2}})$ | D. | $({0,\frac{π}{2}})$ |
12.已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数( )
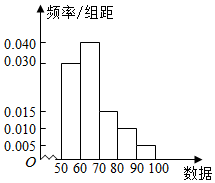

| A. | 63、64、66 | B. | 65、65、67 | C. | 65、64、66 | D. | 64、65、64 |
16.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是(以下k∈Z)( )
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π] | B. | [kπ-$\frac{3}{8}$π,kπ+$\frac{π}{8}$] | C. | [2kπ+$\frac{π}{8}$,2kπ+$\frac{5}{8}$π] | D. | [2kπ-$\frac{3}{8}$π,2kπ+$\frac{π}{8}$] |
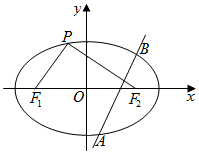 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=$\frac{{\sqrt{2}}}{2}$,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为2.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=$\frac{{\sqrt{2}}}{2}$,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为2.