题目内容
17.设D是△ABC所在平面内一点,且$\overrightarrow{BC}=3\overrightarrow{CD}$,设$\overrightarrow{AD}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=1.分析 根据题意,画出图形,结合图形用向量$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出$\overrightarrow{AD}$,即可求出x、y的值.
解答 解:画出图形,如图所示: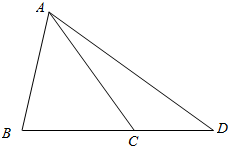
∵$\overrightarrow{BC}$=3$\overrightarrow{CD}$,∴$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\frac{4}{3}$$\overrightarrow{BC}$;
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{4}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AC}$,
∴x=-$\frac{1}{3}$,y=$\frac{4}{3}$;
∴x+y=1.
故答案为:1.
点评 本题考查了平面向量的线性运算问题,也考查了数形结合的应用问题,是基础题目.

练习册系列答案
相关题目
5.已知一次函数f(x)的图象不过第四象限,且f(f(x))=4x+3,则f(x)的表达式为( )
| A. | 2x+1 | B. | -2x-3 | C. | -2x+1 | D. | 2x+3 |
7.设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x,则f(-$\frac{5}{2}$)=( )
| A. | -$\frac{1}{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |