题目内容
若a=(
)
,b=(
)
,c=(
)
,则a,b,c大小关系是 (请用”<”号连接)
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 5 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
考点:指数函数的单调性与特殊点
专题:函数的性质及应用
分析:先比较a,b的大小,根据幂函数的单调性可判定,然后比较a,c的大小,利用指数函数的单调性进行判定,从而得到所求.
解答:
解:∵a=(
)
,b=(
)
,
∴考察幂函数y=x
的单调性,函数y=x
在(0,+∞)上单调递增,
∵
>
,
∴a>b,
∵a=(
)
,c=(
)
,
∴考察指数函数y=(
)x的单调性,函数y=(
)x在(0,+∞)上单调递减,
∵
>
,
∴a<c,
综上所述:b<a<c.
故答案为:b<a<c.
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 5 |
| 2 |
| 3 |
∴考察幂函数y=x
| 2 |
| 3 |
| 2 |
| 3 |
∵
| 1 |
| 2 |
| 1 |
| 5 |
∴a>b,
∵a=(
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴考察指数函数y=(
| 1 |
| 2 |
| 1 |
| 2 |
∵
| 2 |
| 3 |
| 1 |
| 3 |
∴a<c,
综上所述:b<a<c.
故答案为:b<a<c.
点评:本题主要考查利用指数函数的单调性,幂函数的单调性,进行比较大小,同时考查了分析问题的能力,属于基础题.

练习册系列答案
相关题目
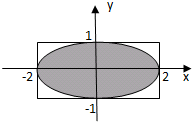 已知椭圆的面积公式为S=πab(其中a为椭圆的长半轴长,b为椭圆的短半轴长),在如图所示矩形框内随机选取400个点,估计这400个点中属于阴影部分的点约有( )
已知椭圆的面积公式为S=πab(其中a为椭圆的长半轴长,b为椭圆的短半轴长),在如图所示矩形框内随机选取400个点,估计这400个点中属于阴影部分的点约有( )| A、100个 | B、200个 |
| C、300个 | D、400个 |
已知数列{an}的首项a1=1,且an=2an-1+1(n≥2),则a6=( )
| A、15 | B、31 | C、62 | D、63 |
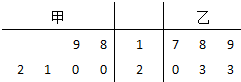 甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示: