题目内容
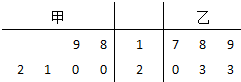 甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:(Ⅰ)写出甲、乙的众数和中位数;
(Ⅱ)计算甲、乙的平均数和方差,依此判断谁更优秀?
考点:茎叶图,众数、中位数、平均数,极差、方差与标准差
专题:概率与统计
分析:(Ⅰ)根据茎叶图读取数据,从小到大排序,处在最中间的两个数的平均数即为中位数,出现次数最多的即为众数;
(Ⅱ)分别根据平均数公式和方差公式求出甲和乙的平均数和方差,平均数相等,然后比较两者方差,方差小的越稳定,成绩就越优秀.
(Ⅱ)分别根据平均数公式和方差公式求出甲和乙的平均数和方差,平均数相等,然后比较两者方差,方差小的越稳定,成绩就越优秀.
解答:
解:(Ⅰ)根据茎叶图可知甲完成的产量为18,19,20,20,21,22,
众数为20,中位数为
=20,
乙完成的产量为17,18,19,20,23,23,
众数为23,中位数为
=19.5;
(Ⅱ)甲的平均数为
(18+19+20+20+21+22)=20,
方差
=
[(18-20)2+(19-20)2+(20-20)2+(20-20)2+(21-20)2+(22-20)2]=
,
乙的平均数为
(17+18+19+20+23+23)=20,
方差
=
[(17-20)2+(18-20)2+(19-20)2+(20-20)2+(23-20)2+(23-20)2]=
,
∵
<
,
∴甲更优秀.
众数为20,中位数为
| 20+20 |
| 2 |
乙完成的产量为17,18,19,20,23,23,
众数为23,中位数为
| 19+20 |
| 2 |
(Ⅱ)甲的平均数为
| 1 |
| 6 |
方差
| s | 2 甲 |
| 1 |
| 6 |
| 5 |
| 3 |
乙的平均数为
| 1 |
| 6 |
方差
| s | 2 乙 |
| 1 |
| 6 |
| 16 |
| 3 |
∵
| s | 2 甲 |
| s | 2 乙 |
∴甲更优秀.
点评:本题考查茎叶图、众数、中位数、平均数和方差,它们分别表示一组数据的特征,方差越小越稳定,属于基础题.

练习册系列答案
相关题目
圆(x-3)2+(y+
)2=1的圆心坐标是( )
| 7 |
| 3 |
A、(3,
| ||
B、(3,-
| ||
C、(-3,
| ||
D、(-
|
△ABC中,sinA=sinB,则三角形的形状为( )
| A、直角△ | B、等腰△ |
| C、等边△ | D、锐角△ |
用秦九韶算法计算多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时v3的值为( )
| A、0 | B、-32 | C、80 | D、-80 |