题目内容
在区间[0,π]上随机取一个数x,则事件“2cos
(sin
+
cos
)≤
+1”发生的概率为 .
| x |
| 2 |
| x |
| 2 |
| 3 |
| x |
| 2 |
| 3 |
考点:几何概型,复合三角函数的单调性
专题:概率与统计
分析:利用辅助角公式将条件进行化简,结合几何概型的概率公式即可得到结论.
解答:
解:2cos
(sin
+
cos
)=sinx+
cosx+
=2sin(x+
)+
,
若2cos
(sin
+
cos
)≤
+1,
则2sin(x+
)+
≤
+1,
即2sin(x+
)≤1,
即sin(x+
)≤
,
∵0≤x≤π,
∴
≤x+
≤
,
则
≤x+
≤
,
解得
≤x≤π,
则事件“2cos
(sin
+
cos
)≤
+1”发生的概率为
=
,
故答案为:
| x |
| 2 |
| x |
| 2 |
| 3 |
| x |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
若2cos
| x |
| 2 |
| x |
| 2 |
| 3 |
| x |
| 2 |
| 3 |
则2sin(x+
| π |
| 3 |
| 3 |
| 3 |
即2sin(x+
| π |
| 3 |
即sin(x+
| π |
| 3 |
| 1 |
| 2 |
∵0≤x≤π,
∴
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
则
| 5π |
| 6 |
| π |
| 3 |
| 4π |
| 3 |
解得
| π |
| 2 |
则事件“2cos
| x |
| 2 |
| x |
| 2 |
| 3 |
| x |
| 2 |
| 3 |
π-
| ||
| π-0 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查几何概型的概率公式的应用,利用辅助角公式将不等式进行化简是解决本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知x,y满足x+2y=2,那么3x+9y的最小值是( )
| A、3 | B、6 | C、9 | D、不存在 |
cos35°cos25°-sin35°sin25°的值为( )
A、
| ||
| B、cos10° | ||
C、-
| ||
| D、-cos10° |
下列说法正确的是( )
A、向量
| ||||||||
B、向量
| ||||||||
C、向量
| ||||||||
| D、单位向量都相等 |
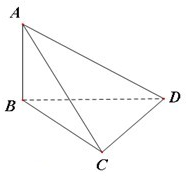 如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为
如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为