题目内容
(文)在30°的二面角的一个面内有一个点,若它到另一个面的距离是10,则它到棱的距离是 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:PO是它到另一个面β的距离,PH它到棱的距离,得出∠PHO为二面角α-l-β的平面角.在RT△PHO中求解即可.
解答:
解: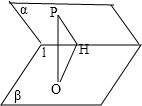 如图所示:
如图所示:
P为二面角α-l-β的一个面α内有一点.
PO是它到另一个面β的距离,PO=10.PH它到棱的距离.
∵PO⊥β,∴PO⊥l,又PH⊥l,∴l⊥面POH,得出l⊥OH,
所以∠PHO为二面角α-l-β的平面角,∠PHO=30°.
在RT△PHO中,PH=
=20.
故答案为:20.
 如图所示:
如图所示:P为二面角α-l-β的一个面α内有一点.
PO是它到另一个面β的距离,PO=10.PH它到棱的距离.
∵PO⊥β,∴PO⊥l,又PH⊥l,∴l⊥面POH,得出l⊥OH,
所以∠PHO为二面角α-l-β的平面角,∠PHO=30°.
在RT△PHO中,PH=
| PO |
| sin∠PHO |
故答案为:20.
点评:本题考查二面角的定义,空间距离求解.考查空间想象能力,推理论证,运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4名同学参加跳高,跳远和100米跑三项决赛,争夺这三项冠军,则冠军结果有( )
| A、34种 | ||
| B、43种 | ||
C、
| ||
D、
|
若函数f(x)=a2-sinx,则f′(x)=( )
| A、-sinx |
| B、-cosx |
| C、2a+sinx |
| D、2a-sinx |
已知点O是边长为1的等边△ABC的外心,则(
+
)•(
+
)等于( )
| OA |
| OB |
| OA |
| OC |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
已知二次函数y=f(x)满足f(2+x)=f(2-x)且函数图象截x轴所得的线段长为8,则函数y=f(x)的零点为( )
| A、2,6 | B、2,-6 |
| C、-2,6 | D、-2,-6 |