题目内容
(B题)在直三棱柱ABC-A1B1C1中,∠BAC=
,AB=AC=AA1=1,D和E分别为棱AC、AB上的动点(不包括端点),若C1E⊥B1D,则线段DE长度的取值范围为 .
| π |
| 2 |
考点:棱柱的结构特征
专题:计算题,作图题,空间向量及应用
分析:由题意建立空间直角坐标系,化为向量问题解答.
解答:
解: 如图建立空间直角坐标系,
如图建立空间直角坐标系,
则B1(1,0,1),D(0,y,0),C1(0,1,1),E(x,0,0).
则
=(x,-1,-1),
=(-1,y,-1).
∵C1E⊥B1D,
∴-x-y+1=0,
即x+y=1(x>0,y>0),
又∵DE=
,
则
≥
=
(当且仅当x=y=0.5时,等号成立),
<1.
故答案为:[
,1).
 如图建立空间直角坐标系,
如图建立空间直角坐标系,则B1(1,0,1),D(0,y,0),C1(0,1,1),E(x,0,0).
则
| C1E |
| B1D |
∵C1E⊥B1D,
∴-x-y+1=0,
即x+y=1(x>0,y>0),
又∵DE=
| x2+y2 |
则
| x2+y2 |
|
| ||
| 2 |
| x2+y2 |
故答案为:[
| ||
| 2 |
点评:本题考查了空间向量的应用,属于基础题.

练习册系列答案
相关题目
若P是直角三角形ABC的斜边BC上的一点,且|
|=2,∠BAP=
,则|
|+
|
|的最小值是( )
| AP |
| π |
| 6 |
| AB |
| 3 |
| AC |
A、4
| ||
| B、4 | ||
C、3+3
| ||
D、3
|
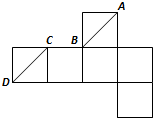 一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中成立的序号是
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中成立的序号是