题目内容
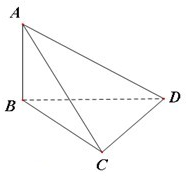如图，AB⊥平面BCD，BD⊥CD，若AB=BC=2BD，则二面角B-AC-D的正弦值为考点：二面角的平面角及求法
专题：空间角
分析：取AC中点E，连EB，过E做AC的垂线交AD于F，由已知得△BFE是直角三角形，∠BEF是二面角B-AC-D的平面角，由此能求出二面角B-AC-D的正弦值．
解答：
解：取AC中点E，连EB，过E做AC的垂线交AD于F
设AB=2a，BC=2a，BD=a，AC=2
，DC=
，
在△ADC中，AF=
，
在△ABD中，AD⊥BF，
又DC⊥BD，由三垂线定理知AD⊥DC，
∴DC⊥面ABD 又BF?面ABD，
∴BF⊥DC，BF⊥面ADC，∴△BFE是直角三角形，
∠BEF是二面角B-AC-D的平面角，
sin∠BEF=
=
．
故答案为：
．
设AB=2a，BC=2a，BD=a，AC=2
| 2a |
| 3a |
在△ADC中，AF=
4
| ||
| 5 |
在△ABD中，AD⊥BF，
又DC⊥BD，由三垂线定理知AD⊥DC，
∴DC⊥面ABD 又BF?面ABD，
∴BF⊥DC，BF⊥面ADC，∴△BFE是直角三角形，
∠BEF是二面角B-AC-D的平面角，
sin∠BEF=
| FB |
| EB |
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：本题考查二面角的正弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
若函数f（x）=a2-sinx，则f′（x）=（ ）
| A、-sinx |
| B、-cosx |
| C、2a+sinx |
| D、2a-sinx |
已知一直线的倾斜角为α，且满足45°≤α≤150°，则直线的斜率的取值范围为（ ）
A、[-
| ||||
B、（-∞，-
| ||||
C、（-∞，-
| ||||
D、[-
|