题目内容
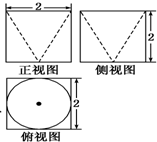
某几何体的三视图如图，则它的体积是 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得该几何体是一个四棱柱挖掉一个圆锥形成的组合体，分别求出棱柱和圆锥底面面积和高，代入可得答案．
解答：
解：由已知中的三视图可得该几何体是一个四棱柱挖掉一个圆锥形成的组合体，
棱柱是一个棱长为2的正方体，故V=8；
圆锥的底面直径为2，故底面面积S=π，高h=2，故V=
，
故组合体的体积为：8-
，
故答案为：8-
棱柱是一个棱长为2的正方体，故V=8；
圆锥的底面直径为2，故底面面积S=π，高h=2，故V=
| 2π |
| 3 |
故组合体的体积为：8-
| 2π |
| 3 |
故答案为：8-
| 2π |
| 3 |
点评：本题考查的知识点是由三视图求体积，其中根据已知的三视图判断出几何体的形状是解答的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
在平面直角坐标系中，A={（x，y）|x2+y2≤1}，B={（x，y）|x≤4，y≥0，3x-4y≥0}则P={（x，y）|x=x1+x2，y=y1+y2，（x1，y1）∈A，（x2，y2）∈B}所表示的区域的面积为（ ）
| A、6 | B、6+π |
| C、12+π | D、18+π |
将函数y=2sin（2x+
）的图象平移后所得的图象对应的函数为y=cos2x，则进行的平移是（ ）
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
