题目内容
已知函数f(x)=2sin(ωx-
)(ω>0)的最小正周期为π.
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移
个单位,再向上平移1个单位,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
| π |
| 3 |
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)直接把周期代入周期公式求ω值,则函数解析式可求,然后利用复合函数的单调性求函数f(x)的单调增区间;
(Ⅱ)利用函数图象的平移得到g(x)的解析式,由g(x)=0求得函数在一个周期内的零点个数,则y=g(x)在区间[0,10π]上零点的个数可求.
(Ⅱ)利用函数图象的平移得到g(x)的解析式,由g(x)=0求得函数在一个周期内的零点个数,则y=g(x)在区间[0,10π]上零点的个数可求.
解答:
解:(Ⅰ)由周期为π,得ω=
=2.
∴f(x)=2sin(2x-
).
由正弦函数的单调增区间得
-
+2kπ≤2x-
≤
+2kπ,
解得kπ-
≤x≤kπ+
,k∈Z.
∴函数f(x)的单调增区间[kπ-
,kπ+
],k∈Z;
(Ⅱ)将函数f(x)的图象向左平移
个单位,再向上平移1个单位,
得到y=2sin2x+1的图象,
∴g(x)=2sin2x+1.
令g(x)=0,得:x=kπ+
或x=kπ+
(k∈Z).
∴函数在每个周期上恰有两个零点,
而[0,10π]恰为10个周期,
故g(x)在[0,10π]上有20个零点.
| 2π |
| π |
∴f(x)=2sin(2x-
| π |
| 3 |
由正弦函数的单调增区间得
-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得kπ-
| π |
| 12 |
| 5π |
| 12 |
∴函数f(x)的单调增区间[kπ-
| π |
| 12 |
| 5π |
| 12 |
(Ⅱ)将函数f(x)的图象向左平移
| π |
| 6 |
得到y=2sin2x+1的图象,
∴g(x)=2sin2x+1.
令g(x)=0,得:x=kπ+
| 7π |
| 12 |
| 11π |
| 12 |
∴函数在每个周期上恰有两个零点,
而[0,10π]恰为10个周期,
故g(x)在[0,10π]上有20个零点.
点评:本题考查y=Asin(ωx+φ)型函数图象的求法,考查了复合函数的单调性的求法,复合函数的单调性满足“同增异减”的原则,考查了函数零点的判断方法,是中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知集合A={0,1,2},则集合B={x+y|x∈A,y∈A}的非空子集的个数为( )
| A、5 | B、30 | C、31 | D、32 |
某产品的广告费用x与销售额y的统计数据如下表:
根据上表可得回归方程
=
x+
中的
为9.4,据此模型预报广告费用为6万元时销售额为( )
| 广告费用x(万元) | 3.5 | 3.8 | 4 | 4.7 |
| 销售费用x(万元) | 27 | 37 | 47 | 49 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、63.6万元 |
| B、58.8万元 |
| C、67.7万元 |
| D、72.0万元 |
函数y=x2+1在x=2处的导数是( )
| A、5 | B、4 | C、3 | D、2 |
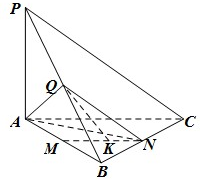 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
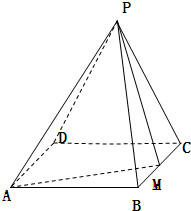 如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=
如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=