题目内容
一个质地均匀的正四面体玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:
分析:由题意知,本题是一个古典概型,试验发生包含的事件数可以利用分步计数原理得到,满足条件的事件是色子着地的一面上的数字之积大于6,可以借助与数对,列举出所有结果,根据古典概型概率公式得到结果.
解答:
解:由题意知,本题是一个古典概型,
试验发生包含的事件数4×4=16,
满足条件的事件是连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数,
可以列举出事件(1,2),(1,4),(2,1),(2,2),(2,3),(2,4),(3,2),(3,4),(4,1),(4,2),(4,3),(4,4)共有12种结果,
根据古典概型的概率公式得到概率是
=
,
故选B.
试验发生包含的事件数4×4=16,
满足条件的事件是连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数,
可以列举出事件(1,2),(1,4),(2,1),(2,2),(2,3),(2,4),(3,2),(3,4),(4,1),(4,2),(4,3),(4,4)共有12种结果,
根据古典概型的概率公式得到概率是
| 12 |
| 16 |
| 3 |
| 4 |
故选B.
点评:本题考查古典概型的概率问题,是一个基础题,题目的所有事件和满足条件的事件都比较容易做出,这种题目出现时不能丢分.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
在钝角三角形ABC中,a=1,b=2,则最大边c的取值范围是( )
A、(
| ||
B、(
| ||
| C、(2,3) | ||
D、(
|
已知命题p:对任意x∈R,总有x2≥0; q:x=2是方程x+3=0的根,则下列命题为真命题的是( )
| A、¬p∧q | B、p∧¬q |
| C、¬p∧¬q | D、p∧q |
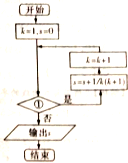
如图是求
+
+
+…+
的值的程序框图,则判断框①中应填( )
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |

| A、k≤99? |
| B、k<99? |
| C、k≤100? |
| D、k<98? |
圆x2+y2-2x+4y+1=0和圆x2+y2-6x+2y+9=0的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内切 |
如果圆(x-a)2+(y-a)2=8上总存在到原点的距离为
的点,则实数a的取值范围是( )
| 2 |
| A、(-3,-1)∪(1,3) |
| B、(-3,3) |
| C、[-1,1] |
| D、[-3,-1]∪[1,3] |