题目内容
圆x2+y2-2x+4y+1=0和圆x2+y2-6x+2y+9=0的位置关系是（ ）
| A、外离 | B、外切 | C、相交 | D、内切 |
考点：圆与圆的位置关系及其判定
专题：直线与圆
分析：求出两个圆的标准方程和两个圆的圆心距，再根据圆心距大于半径之差且小于半径之和，可得结论．
解答：
解：圆x2+y2-2x+4y+1=0即 （x-1）2+（y+2）2=4，表示以（1，-2）为圆心、半径等于2的圆．
圆x2+y2-6x+2y+9=0 即 （x-3）2+（y+1）2=1表示以（3，-1）为圆心、半径等于1的圆．
由于两个圆的圆心距d=
=
，大于半径之差且小于半径之和，
故两个圆相交，
故选：C．
圆x2+y2-6x+2y+9=0 即 （x-3）2+（y+1）2=1表示以（3，-1）为圆心、半径等于1的圆．
由于两个圆的圆心距d=
| (3-1)2+(-1+2)2 |
| 5 |
故两个圆相交，
故选：C．
点评：本题主要考查圆的标准方程，两圆的位置关系的判定方法，两点间的距离公式的应用，属于基础题．
练习册系列答案
相关题目
下列式子正确的是（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、λ（μa）=（λμ）
| ||||||||||||
D、
|
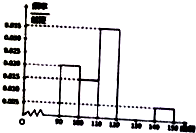某校高三数学竞赛初赛考试后，对考生的成绩进行统计（考生成绩均不低于90分，满分为150分），将成绩按如下方式分成六组，第一组[90，100）、第二组[100，110）…，第六组[140，150]，如图为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人．