题目内容
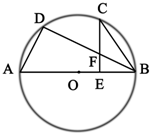 如图:AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图:AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.(Ⅰ)求证:CF=BF;
(Ⅱ)若AD=4,⊙O的半径为6,求BC的长.
考点:与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)法一:连接CO交BD于点M,由已知条件推导出Rt△CEO≌Rt△BMO,由此能证明CF=BF.
(Ⅰ)法二:延长CE 交圆O于点N,连接BN,由已知条件推导出∠CBD=∠CNB,由此能证明CF=BF.
(Ⅱ)由O,M分别为AB,BD的中点,得到EB,由此以求出BC.
(Ⅰ)法二:延长CE 交圆O于点N,连接BN,由已知条件推导出∠CBD=∠CNB,由此能证明CF=BF.
(Ⅱ)由O,M分别为AB,BD的中点,得到EB,由此以求出BC.
解答:
(Ⅰ)证法一:连接CO交BD于点M,如图1…(1分)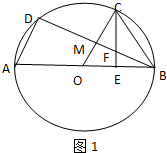
∵C为弧BD的中点,∴OC⊥BD
又∵OC=OB,∴Rt△CEO≌Rt△BMO…(2分)
∴∠OCE=∠OBM…(3分)
又∵OC=OB,∴∠OCB=∠OBC…(4分)
∴∠FBC=∠FCB,∴CF=BF…(5分)
(Ⅰ)证法二:延长CE 交圆O于点N,连接BN,如图2…(1分)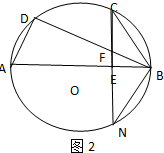
∵AB是直径且CN⊥AB于点E
∴∠NCB=∠CNB…(2分)
又∵弧CD=弧BC,∴∠CBD=∠CNB…(3分)
∴∠NCB=∠CBD
即∠FCB=∠CBF…(4分)
∴CF=BF…(5分)
(Ⅱ)∵O,M分别为AB,BD的中点
∴OM=2=OE
∴EB=4…(7分)
在Rt△COE中,CE=
=4
…(9分)
∴在Rt△CEB中,BC=
=4
.…(10分)

∵C为弧BD的中点,∴OC⊥BD
又∵OC=OB,∴Rt△CEO≌Rt△BMO…(2分)
∴∠OCE=∠OBM…(3分)
又∵OC=OB,∴∠OCB=∠OBC…(4分)
∴∠FBC=∠FCB,∴CF=BF…(5分)
(Ⅰ)证法二:延长CE 交圆O于点N,连接BN,如图2…(1分)

∵AB是直径且CN⊥AB于点E
∴∠NCB=∠CNB…(2分)
又∵弧CD=弧BC,∴∠CBD=∠CNB…(3分)
∴∠NCB=∠CBD
即∠FCB=∠CBF…(4分)
∴CF=BF…(5分)
(Ⅱ)∵O,M分别为AB,BD的中点
∴OM=2=OE
∴EB=4…(7分)
在Rt△COE中,CE=
| OC2-OE2 |
| 2 |
∴在Rt△CEB中,BC=
| CE2+BE2 |
| 3 |
点评:本题考查线段相等的证明,考查线段长的求法,解题时要认真审题,注意圆的简单性质的合理运用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
若集合A={y|y=ax,a>0,x≠1},则∁RA等于( )
| A、(-∞,0) |
| B、(-∞,0] |
| C、(0,+∞) |
| D、[0,+∞) |
 证明:card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(A∩C)-card(B∩C)+card(A∩B∩C)
证明:card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(A∩C)-card(B∩C)+card(A∩B∩C)