题目内容
已知双曲线C:
-
=1的右焦点为F,P是第一象限内C上的点,Q为双曲线左准线上的点,若OP垂直平分FQ,则双曲线的离心率e的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:OP垂直平分FQ,O到F和Q的距离相等,即c2=
+p2,求出OP所在直线方程,直线必与双曲线相交,且交点的横坐标和纵坐标均大于零,即可得出结论.
| a4 |
| c2 |
解答:
解:右焦点F(c,0),左准线与x轴的交点B,
设P(m,n),m>0,n>0,m、n满足
-
=1①
左准线方程x=-
,令Q(-
,p)
OP垂直平分FQ,O到F和Q的距离相等,即c2=
+p2②
设FQ中点A,则A(
,
),OP所在直线方程:y=
x
由②得:p=
则有y=
x③
该直线必与双曲线相交,且交点的横坐标和纵坐标均大于零
将③代入①式:x2(
-
)-1=0,
∴2(
)4+(
)2-1>0
∴(
)2>
,
∴e=
=
>
,
故答案为:e>
.
设P(m,n),m>0,n>0,m、n满足
| m2 |
| a2 |
| n2 |
| b2 |
左准线方程x=-
| a2 |
| c |
| a2 |
| c |
OP垂直平分FQ,O到F和Q的距离相等,即c2=
| a4 |
| c2 |
设FQ中点A,则A(
| b2 |
| 2c |
| p |
| 2 |
| pc |
| b2 |
由②得:p=
b
| ||
| c |
| ||
| b |
该直线必与双曲线相交,且交点的横坐标和纵坐标均大于零
将③代入①式:x2(
| 1 |
| a2 |
| c2+a2 |
| b4 |
∴2(
| a |
| b |
| a |
| b |
∴(
| a |
| b |
| 1 |
| 2 |
∴e=
| c |
| a |
1+
|
| 3 |
故答案为:e>
| 3 |
点评:本题考查双曲线的性质,考查直线与双曲线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知O为坐标原点,A(1,2),点P(x,y)满足约束条件
,则Z=
•
的最大值为( )
|
| OA |
| OP |
| A、-2 | B、-1 | C、1 | D、2 |
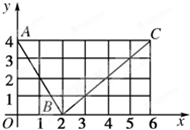 如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).
如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).