题目内容
已知O为坐标原点，A（1，2），点P（x，y）满足约束条件
，则Z=
•
的最大值为（ ）
|
| OA |
| OP |
| A、-2 | B、-1 | C、1 | D、2 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于点P（x，y）满足约束条件
，画出可行域．设P（x，y）．可得Z=
•
=x+2y，化为y=-
x+
，当此直线经过点M（0，1）时，Z取得最大值．
|
| OA |
| OP |
| 1 |
| 2 |
| Z |
| 2 |
解答：
解：由于点P（x，y）满足约束条件
，画出可行域．
设P（x，y）．
则Z=
•
=x+2y，
化为y=-
x+
，
当此直线经过点M（0，1）时，Z取得最大值=0+1×2=2．
∴Z=
•
的最大值为2．
故选：D．
|
设P（x，y）．
则Z=
| OA |
| OP |
化为y=-
| 1 |
| 2 |
| Z |
| 2 |
当此直线经过点M（0，1）时，Z取得最大值=0+1×2=2．
∴Z=
| OA |
| OP |
故选：D．
点评：本题考查了利用线性规划的可行域求最大值，考查了数形结合的思想方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
若a＞b＞c，a+2b+3c=0，则（ ）
| A、ab＞ac |
| B、ac＞bc |
| C、ab＞bc |
| D、a|b|＞c|b| |
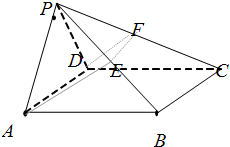四棱锥P-ABCD中，底面ABCD是∠DAB=60°的菱形，侧面PAD为正三角形．