Question

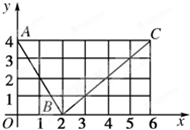如图所示折线段ABC，其中A、B、C的坐标分别为（0，4），（2，0），（6，4）．
（1）若一抛物线g（x）恰好过A，B，C三点，求g（x）的解析式．
（2）函数f（x）的图象刚好是折线段ABC，求f（f（0））的值和函数f（x）的解析式．

Answer 1

考点：函数解析式的求解及常用方法

专题：函数的性质及应用

分析：（1）设抛物线方程为g（x）=ax²+bx+c，则

4=c 4a+2b+c=0 36a+6b+c=4

，解得即可．
（2）由图象可知：f（0）=4，f（4）=2，可得f（f（0））．
当0≤x≤2时，线段AB经过点A（0，4），B（2，0），利用斜截式即可得出；．
当2≤x≤6时，线段BC经过点C（6，4），B（2，0利用点斜式即可得出．

解答： 解：（1）设抛物线方程为g（x）=ax²+bx+c，
则

4=c 4a+2b+c=0 36a+6b+c=4

，解得c=4，a=

1

2

，b=-3．
∴g（x）=

1

2

x2-3x+4．
（2）由图象可知：f（0）=4，f（4）=2，∴f（f（0））=2．
当0≤x≤2时，线段AB经过点A（0，4），B（2，0），∴y=

4-0

0-2

x+4，即y=-2x+4．
当2≤x≤6时，线段BC经过点C（6，4），B（2，0），∴y=

4-0

6-2

(x-2)，即y=x-2．
∴f（x）=

-2x+4，x∈[0，2] x-2，x∈(2，6]

．

点评：本题考查了利用“待定系数法”求二次函数的解析式、分段函数的解析式求法，考查了计算能力，属于基础题．