题目内容
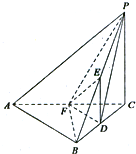 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.(1)证明:PC∥平面DEF;
(2)证明:平面PBF⊥平面PAC;
(3)若PC=AB=2,求三棱锥P-DEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由D,E,分别是BC,PB的中点,得DE∥PC,由此能证明PC∥平面DEF.
(2)先根据PC⊥平面ABC,BF?平面ABC得到PC⊥BF;再结合BF⊥AC即可得到BF⊥平面PAC,进而证明平面PBF⊥平面PAC.
(3)直接根据D,E,F分别为BC,PB,CA的中点,把所求体积进行转化;转化为
VP-BDF即可求出结论.
(2)先根据PC⊥平面ABC,BF?平面ABC得到PC⊥BF;再结合BF⊥AC即可得到BF⊥平面PAC,进而证明平面PBF⊥平面PAC.
(3)直接根据D,E,F分别为BC,PB,CA的中点,把所求体积进行转化;转化为
| 1 |
| 2 |
解答:
(1)证明:在△PBC中,∵D,E,分别是BC,PB的中点,
∴DE∥PC,
∵PC不包含于平面DEF,DE?平面DEF,
∴PC∥平面DEF.
(2)证明:∵PC⊥平面ABC,BF?平面ABC.
∴PC⊥BF.由条件得BF⊥AC,PC∩AC=C.
∴BF⊥平面PAC,BF?平面PBF,
∴平面PBF⊥平面PAC.
(3)解:∵D,E,F分别为BC,PB,CA的中点.
∴VP-DEF=VC-DEF=VE-DFC=VE-BDF
=
VP-BDF
=
×
×S△BDF•PC
=
×
×
S△ABC•PC
=
×
×
×
×2×2×
×2
=
.
∴DE∥PC,
∵PC不包含于平面DEF,DE?平面DEF,
∴PC∥平面DEF.
(2)证明:∵PC⊥平面ABC,BF?平面ABC.
∴PC⊥BF.由条件得BF⊥AC,PC∩AC=C.
∴BF⊥平面PAC,BF?平面PBF,
∴平面PBF⊥平面PAC.
(3)解:∵D,E,F分别为BC,PB,CA的中点.
∴VP-DEF=VC-DEF=VE-DFC=VE-BDF
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 12 |
点评:本题主要考查平面与平面垂直的判定以及棱锥体积的求法.棱锥体积的求法常用转化思想,变为易求的几何体的体积,考查计算能力.

练习册系列答案
相关题目
下列关于函数f(x)=(x+1)|x|的单调性的叙述中,正确的是( )
| A、f(x)在定义域上单调递增 | ||
| B、f(x)在定义域上单调递减 | ||
| C、f(x)在(-∞,0)上是增函数,在(0,+∞)上是减函数 | ||
D、f(x)在(-
|
当a>0时,函数f(x)=(x2-ax)ex的图象大致是( )
A、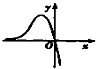 |
B、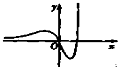 |
C、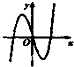 |
D、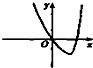 |