题目内容
解关于a的方程:a(a3-3a+10)-8=0.
考点:函数的零点
专题:计算题
分析:将a(a3-3a+10)-8=0转化为(a-1)(a3+a2-2a+8)=0,解出即可.
解答:
解:∵a(a3-3a+10)-8=0,
∴a4-3a2+10a-8=0,
∴a4-a2-2a2+2a+8a-8=0,
∴(a-1)(a3+a2-2a+8)=0,
∴a=1.
∴a4-3a2+10a-8=0,
∴a4-a2-2a2+2a+8a-8=0,
∴(a-1)(a3+a2-2a+8)=0,
∴a=1.
点评:本题考查了解高次方程问题,一般采用因式分解的方法求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设α,β为两个不同平面,m、n为两条不同的直线,且m?α,n?β,有两个命题:P:若m∥n,则α∥β;q:若m⊥β,则α⊥β.那么( )
| A、“¬p或q”是假命题 |
| B、“¬p且q”是真命题 |
| C、“p或¬q”是真命题 |
| D、“¬p且q”是真命题 |
下列说法正确的是( )
| A、若p∧q为假命题,则p,q均为假命题 | ||||||||||||
| B、设实数a,b,c满足a+b+c=0,则a,b,c中至少有一个不小于0 | ||||||||||||
C、若
| ||||||||||||
| D、函数y=log2(x2-2x)的单调增区间是[1,+∞) |
函数y=
的图象大致是( )
| sin6x |
| 2x-2-x |
A、 |
B、 |
C、 |
D、 |
不等式(x-1)
≥0的解集是( )
| x+3 |
| A、{x|x>1} |
| B、{x|x≥1或x=-3} |
| C、{x|x≥1} |
| D、{x|x≥-3且x≠1} |




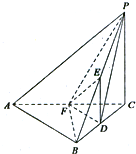 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.