题目内容
已知数列A:a1,a2,a3,…,an(0≤a1<a2<a3<…<an,n≥3,n∈N*)具有性质P:对任意的i,j(1≤i≤j≤n,i,j∈N*),aj+ai与aj-ai两数中至少有一个是数列A中的项,现下列命题正确的是: .(写出所有正确答案的序号)
①数列A:0,1,3与数列B:0,2,4,6都具有性质P;
②a1=0;
③2(a1+a2+a3+…+an)=nan;
④当n=5时,a1,a2,a3,a4,a5成等差数列.
①数列A:0,1,3与数列B:0,2,4,6都具有性质P;
②a1=0;
③2(a1+a2+a3+…+an)=nan;
④当n=5时,a1,a2,a3,a4,a5成等差数列.
考点:命题的真假判断与应用
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:根据数列:a1,a2,…an(0≤a1<a2…<an),n≥3时具有性质P,对任意i,j(1≤i<j≤n),aj+ai与aj-ai两数中至少有一个是该数列中的一项,逐一验证即可.
解答:
解:对于①因为1+3=4,3-1=2,都不是数列A中的项,故命题①错误;
对于②,考查该数列中的最大项an,显然an+an=2an不是数列中的项,则必有an-an=0属于该数列,故0∈A,且a1=0,故②正确;
对于③若数列A具有该性质P,设an是最大项,则具有性质ai+an(1<i≤n,i∈N*),不在A中,则an-ai是数列A中的项,则依题意:an-an<an-an-1<an-an-2<…<an-a2<an-a1,则由给的数列A的性质可知;an-an=a1,an-an-1=a2,an-an-2=a3,…an-a2=an-1,an-a1=an,将前面n个式子相加得:nan-(a1+a2+a3+…an-1+an)=a1+a2+a3+…+an-1+an,故nan=2(a1+a2+a3+…an-1+an),故③正确;
对于④,当n=5时,因为a1=0,a2-a1=a2,且
⇒
⇒2a3=a4+a2⇒2a3=a4+a2,而a4+a3>2a3=a5不是数列A中的项,则a4-a3是数列A中的项,
所以a1<a4-a3<a5-a3=a3,所以a4-a3=a2,所以a2-a1=a3-a2=a4-a5=a5-a4,故④成立.
故答案为:②③④
对于②,考查该数列中的最大项an,显然an+an=2an不是数列中的项,则必有an-an=0属于该数列,故0∈A,且a1=0,故②正确;
对于③若数列A具有该性质P,设an是最大项,则具有性质ai+an(1<i≤n,i∈N*),不在A中,则an-ai是数列A中的项,则依题意:an-an<an-an-1<an-an-2<…<an-a2<an-a1,则由给的数列A的性质可知;an-an=a1,an-an-1=a2,an-an-2=a3,…an-a2=an-1,an-a1=an,将前面n个式子相加得:nan-(a1+a2+a3+…an-1+an)=a1+a2+a3+…+an-1+an,故nan=2(a1+a2+a3+…an-1+an),故③正确;
对于④,当n=5时,因为a1=0,a2-a1=a2,且
|
|
所以a1<a4-a3<a5-a3=a3,所以a4-a3=a2,所以a2-a1=a3-a2=a4-a5=a5-a4,故④成立.
故答案为:②③④
点评:本题属于创新题,要准确理解A的性质,抓住特殊项,结合性质去推理,才能较好地解决此题.

练习册系列答案
相关题目
(文)若a∈R,则“a2>a”是“a>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
不等式(x-1)
≥0的解集是( )
| x+3 |
| A、{x|x>1} |
| B、{x|x≥1或x=-3} |
| C、{x|x≥1} |
| D、{x|x≥-3且x≠1} |
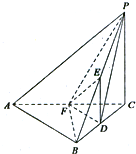 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.