题目内容
已知函数f(x)=ax2+(2a+1)x+1-3a,其中,a≠0.若g(x)=
,是否存在实数a,使得g[g(x)]=0只有一个实数根?若存在,请求出a的值或者a的取值范围,若不存在,请说明理由.
| f(x) |
| a |
考点:函数的零点
专题:函数的性质及应用
分析:假设存在实数a,使得g[g(x)]=0只有一个实数根,得方程解出即可.
解答:
解:假设存在实数a,使得g[g(x)]=0只有一个实数根,
∵f(x)=ax2+(2a+1)x+1-3a(a≠0),
∴g(x)=f'(x)=2ax+2a+1,
又∵g[g(x)]=0,
∴g[g(x)]=g(2ax+2a+1)=0,
∵a≠0,
∴x=-
=-1-
,
综上所述,存在实数a,使得g[g(x)]=0只有一个实数根.
∵f(x)=ax2+(2a+1)x+1-3a(a≠0),
∴g(x)=f'(x)=2ax+2a+1,
又∵g[g(x)]=0,
∴g[g(x)]=g(2ax+2a+1)=0,
∵a≠0,
∴x=-
| 2a+1 |
| 2a |
| 1 |
| 2a |
综上所述,存在实数a,使得g[g(x)]=0只有一个实数根.
点评:本题考查了函数的零点问题,考查导数的应用,是一道中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
设m、n是两条不同的直线,α、β是两个不同的平面,下列命题中错误的是( )
| A、若m⊥α,m∥n,n∥β,则α⊥β |
| B、若α⊥β,m?α,m⊥β,则m∥α |
| C、若m⊥β,m?α,则α⊥β |
| D、若α⊥β,m?α,n?β,则m⊥n |
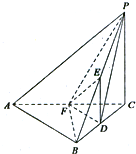 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.