题目内容
求函数y=
+
,x∈R的最大值、最小值,并求使函数取得最大值、最小值的x的集合.
| 2 |
| sinx |
| π |
考点:三角函数的最值
专题:三角函数的图像与性质
分析:利用正弦函数的单调性与最值即可求得函数y=
+
,x∈R的最大值和最小值.并求取得最大值,最小值时x的集合.
| 2 |
| sinx |
| π |
解答:
解:∵-1≤sinx≤1,
∴-
≤
≤
,
∴
-
≤
+
≤
+
,
∴y=
+
的最大值为
+
,当x=2kπ+
,k∈Z时函数取得最大值.
函数取得最大值时x的集合{x=2kπ+
,k∈Z}.
最小值为
-
;当x=2kπ-
,k∈Z时函数取得最小值.
函数取得最小值x的集合{x=2kπ-
,k∈Z}.
∴-
| 1 |
| π |
| sinx |
| π |
| 1 |
| π |
∴
| 2 |
| 1 |
| π |
| 2 |
| sinx |
| π |
| 2 |
| 1 |
| π |
∴y=
| 2 |
| sinx |
| π |
| 2 |
| 1 |
| π |
| π |
| 2 |
函数取得最大值时x的集合{x=2kπ+
| π |
| 2 |
最小值为
| 2 |
| 1 |
| π |
| π |
| 2 |
函数取得最小值x的集合{x=2kπ-
| π |
| 2 |
点评:本题考查正弦函数的单调性与最值,掌握正弦函数的性质是关键,属于基础题.

练习册系列答案
相关题目
在△ABC中,内角A,B,C所对的边分别是a,b,c,已知b-c=
a,2sinB=3sinC,则cosA=( )
| 1 |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
(文)若a∈R,则“a2>a”是“a>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
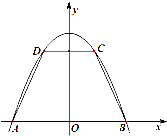 如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.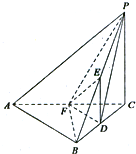 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.