题目内容
定义在(-∞,+∞)上的奇函数f(x)在(-∞,0]上是增函数,试解关于x的不等式:f(1-x)+f(1-x2)>0.
考点:奇偶性与单调性的综合
专题:综合题,函数的性质及应用
分析:利用奇函数f(x)是定义在[-1,1]上的增函数,可将函数符号“脱去”,从而转化为不等式组,进而可求得不等式f(x-1)+f(1-x2)<0的解集.
解答:
解:不等式f(1-x)+f(1-x2)>0可化为:f(1-x)>-f(1-x2)
∵f(x)是奇函数
∴f(1-x)>f(-1+x2)
∵函数f(x)是定义在[-1,1]上的增函数,
∴-1≤-1+x2<1-x≤1
∴0≤x<1
∴不等式f(1-x)+f(1-x2)>0的解集为[0,1).
∵f(x)是奇函数
∴f(1-x)>f(-1+x2)
∵函数f(x)是定义在[-1,1]上的增函数,
∴-1≤-1+x2<1-x≤1
∴0≤x<1
∴不等式f(1-x)+f(1-x2)>0的解集为[0,1).
点评:本题将函数的奇偶性与单调性巧妙结合,考查不等式的解法,解题的关键是利用函数的奇偶性与单调性,将所求不等式进行转化.

练习册系列答案
相关题目
如果执行如图的程序框图,那么输出的S等于( )


| A、45 | B、55 | C、90 | D、110 |
设α,β为两个不同平面,m、n为两条不同的直线,且m?α,n?β,有两个命题:P:若m∥n,则α∥β;q:若m⊥β,则α⊥β.那么( )
| A、“¬p或q”是假命题 |
| B、“¬p且q”是真命题 |
| C、“p或¬q”是真命题 |
| D、“¬p且q”是真命题 |
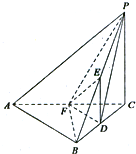 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.