题目内容
函数f（x）=x2-3x+2在区间（1，2）内的函数值为（ ）
| A、大于等于0 | B、等于0 |
| C、大于0 | D、小于0 |
考点：二次函数的性质
专题：函数的性质及应用
分析：由已知f（x）=x2-3x+2=（x-1）（x-2），由1＜x＜2，可知x-1＞0，x-2＜0，可得函数值的符号．
解答：
解：由已知得f（x）=x2-3x+2=（x-1）（x-2），
因为1＜x＜2，所以x-1＞0，x-2＜0，
所以f（x）＜0，即f（x）=x2-3x+2在区间（1，2）内的函数值小于0；
故选D．
因为1＜x＜2，所以x-1＞0，x-2＜0，
所以f（x）＜0，即f（x）=x2-3x+2在区间（1，2）内的函数值小于0；
故选D．
点评：本题考查了二次函数在某个区间的函数值符号的确定；可以利用因式分解法确定每个因式的符号，也可以结合图象判断．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
设函数f（x）=logax（a＞0，且a≠1）在（0，+∞）上单调递增，则f（a+1）与f（2）的大小关系是（ ）
| A、f（a+1）=f（2） |
| B、f（a+1）＞f（2） |
| C、f（a+1）＜f（2） |
| D、不确定 |
要得到函数y=
cosx的图象，只需将函数y=
cos（2x+
）的图象上所有的点（ ）
| 2 |
| 2 |
| π |
| 4 |
A、横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标缩短到原来的
| ||||
D、横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动
|
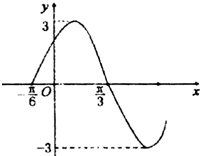
如图所示是y=Asin（ωx+φ）的图象（其中A＞0，ω＞0，|φ|≤
）一部分，则其解析表达式为（ ）
| π |
| 2 |
A、y=3cos（2x+
| ||
B、y=3cos（2x-
| ||
C、y=3sin（2x+
| ||
D、y=3sin（2x-
|
函数y=f（x）在区间（-2，2）上的图象是连续不断的，且方程f（x）=0在（-2，2）上仅有一个实根x=0，则f（-1）f（1）的值（ ）
| A、大于0 |
| B、小于0 |
| C、等于0 |
| D、与0的大小关系无法确定 |