题目内容
设t>0,函数f(x)=
的值域为M,若4∉M,则t的取值范围是 .
|
考点:函数的值域
专题:函数的性质及应用
分析:根据函数f(x)=
,可得0<y<2t,或y≤log
,
由值域为M,4∉M,可得:2t≤4,且log
,<4,即可解出t 的范围.
|
t
|
由值域为M,4∉M,可得:2t≤4,且log
t
|
解答:
解:∵函数f(x)=
可得0<y<2t,或y≤log
,
∴值域为:{y|0<y<2t,或y≤log
}
∵域为M,若4∉M,
∴2t≤4,且log
,<4,
可解得:
<y≤2
故答案为:(
,2]
|
t
|
∴值域为:{y|0<y<2t,或y≤log
t
|
∵域为M,若4∉M,
∴2t≤4,且log
t
|
可解得:
| 1 |
| 16 |
故答案为:(
| 1 |
| 16 |
点评:本题考察了分段函数的值域,解对数不等式等知识,注意单调性的运用.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知集合M={y|y=-x2+1,x∈R},N={y|y=x2,x∈R},全集I=R,则M∪N等于( )
A、{(x,y)|x=±
| ||||||
B、{(x,y)|x≠±
| ||||||
| C、{y|y≤0,或y≥1} | ||||||
| D、R |
函数f(x)=x2-3x+2在区间(1,2)内的函数值为( )
| A、大于等于0 | B、等于0 |
| C、大于0 | D、小于0 |
方程lnx=6-2x的根必定属于区间( )
| A、(-2,1) | ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
将函数y=sin(4x-
)的图象先向左平移
,然后将所得图象上所有的点的横坐标变为原来的4倍(纵坐标不变),则所得到的图象对应的函数解析式为( )
| π |
| 3 |
| π |
| 12 |
| A、y=-cosx | ||
| B、y=sin4x | ||
| C、y=sinx | ||
D、y=sin(x-
|
在△ABC中,若AB=2,AC2+BC2=8,则△ABC面积的最大值为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
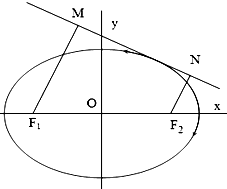 设点F1(-c,0),F2(c,0)分别是椭圆C:
设点F1(-c,0),F2(c,0)分别是椭圆C: