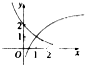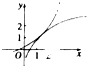题目内容
函数y=f(x)在区间(-2,2)上的图象是连续不断的,且方程f(x)=0在(-2,2)上仅有一个实根x=0,则f(-1)f(1)的值( )
| A、大于0 |
| B、小于0 |
| C、等于0 |
| D、与0的大小关系无法确定 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据函数y=f(x)在区间(-2,2)上的图象是连续不断的,且方程f(x)=0在(-2,2)上仅有一个实根x=0,画出图象即可判断出.
解答:
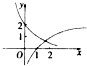
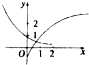
解:由于函数y=f(x)在区间(-2,2)上的图象是连续不断的,且方程f(x)=0在(-2,2)上仅有一个实根x=0,
可得图象:
因此f(-1)f(1)的值与0的大小关系不正确.
故选:D.
可得图象:

因此f(-1)f(1)的值与0的大小关系不正确.
故选:D.
点评:本题考查了函数零点存在判定定理,考查了数形结合的思想方法,属于基础题.

练习册系列答案
相关题目
已知A={y|y=log2x,x<2},B={y|y=(
)x,x<1},则A∩B=( )
| 1 |
| 2 |
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(
|
关于方程|log2x|=lg(x+1)的两个根x1,x2(x1<x2)以下说法正确的是( )
| A、x1+x2>2 |
| B、x1x2>2 |
| C、0<x1x2<1 |
| D、1<x1+x2<2 |
函数f(x)=x2-3x+2在区间(1,2)内的函数值为( )
| A、大于等于0 | B、等于0 |
| C、大于0 | D、小于0 |
某设备的使用年限x与所支出的总费用y(万元)统计数据如下表
据上表可得回归方程
=
x+
中的
=0.7,据此预测设备使用年限为6年时总费用为( )
| 使用年限x | 1 | 2 | 3 | 4 |
| 总费用y | 1.5 | 2 | 3 | 3.5 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、4.95万元 |
| B、5.2万元 |
| C、4.35万元 |
| D、4.9万元 |
将函数y=sin(4x-
)的图象先向左平移
,然后将所得图象上所有的点的横坐标变为原来的4倍(纵坐标不变),则所得到的图象对应的函数解析式为( )
| π |
| 3 |
| π |
| 12 |
| A、y=-cosx | ||
| B、y=sin4x | ||
| C、y=sinx | ||
D、y=sin(x-
|
已知集合A={1,2,4},B={2,3,4},那么集合A∪B等于( )
| A、{1,2} |
| B、{2,4} |
| C、{1,2,3,4} |
| D、{1,2,3} |