题目内容
要得到函数y=
cosx的图象,只需将函数y=
cos(2x+
)的图象上所有的点( )
| 2 |
| 2 |
| π |
| 4 |
A、横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标缩短到原来的
| ||||
D、横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:先把函数y=
cos(2x+
)的图象进行伸缩变换得y=
cos(x+
),再进行平移变换得y=
cosx的图象.
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
解答:
解:把函数y=
cos(2x+
)的图象上所有的点横坐标伸长到原来的2倍(纵坐标不变),得到图象所对应的函数解析式为y=
cos(x+
),再把该图象向右平行移动
个单位长度得到函数y=
cosx的图象.
故选:D.
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
故选:D.
点评:本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减,是基础题.

练习册系列答案
相关题目
关于方程|log2x|=lg(x+1)的两个根x1,x2(x1<x2)以下说法正确的是( )
| A、x1+x2>2 |
| B、x1x2>2 |
| C、0<x1x2<1 |
| D、1<x1+x2<2 |
函数f(x)=x2-3x+2在区间(1,2)内的函数值为( )
| A、大于等于0 | B、等于0 |
| C、大于0 | D、小于0 |
将函数y=sin(4x-
)的图象先向左平移
,然后将所得图象上所有的点的横坐标变为原来的4倍(纵坐标不变),则所得到的图象对应的函数解析式为( )
| π |
| 3 |
| π |
| 12 |
| A、y=-cosx | ||
| B、y=sin4x | ||
| C、y=sinx | ||
D、y=sin(x-
|
用反证法证明命题“若a、b、c∈(0,1),则(1-a)b,(1-b)c,(1-c)a不能都大于
”时,假设( )
| 1 |
| 4 |
A、(1-a)b,(1-b)c,(1-c)a都不大于
| ||
B、(1-a)b,(1-b)c,(1-c)a都小于或等于
| ||
C、(1-a)b,(1-b)c,(1-c)a都大于
| ||
D、(1-a)b,(1-b)c,(1-c)a不能都小于或等于
|
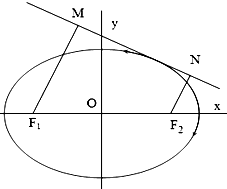 设点F1(-c,0),F2(c,0)分别是椭圆C:
设点F1(-c,0),F2(c,0)分别是椭圆C: