题目内容
17．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x+1，}&{x＞0}\\{a，}&{x=0}\\{g（2x），}&{x＜0}\end{array}\right.$为奇函数，则a=0，f（g（-2））=-25．分析 利用分段函数，结合函数的奇偶性，即可得出结论．
解答 解：由题意，a=f（0）=0．
设x＜0，则-x＞0，f（-x）=x2-2x+1=-f（x），
∴g（2x）=-x2+2x-1，
∴g（-2）=-4，
∴f（g（-2））=f（-4）=-16-8-1=-25．
故答案为：0，-25．
点评 本题考查分段函数，考查函数的奇偶性，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
7．“a＞b，c＞0”是“ac＞bc”的（ ）条件．
| A． | 必要不充分 | B． | 充分不必要 | ||
| C． | 充要 | D． | 既不充分也不必要 |
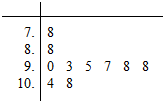某射击爱好者想提高自己的射击水平，制订了了一个训练计划，为了了解训练效果，执行训练计划前射击了10发子弹（每发满分为10.9环），计算出成绩中位数为9.65环，总成绩为95.1环，成绩标准差为1.09环，执行训练计划后也射击了10发子弹，射击成绩茎叶图如图所示．