题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,在同一周期内,当x=
时,f(x)取得最大值2;当x=
时,f(x)取得最小值-2.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若x∈[0,
]时,求函数f(x)的单调增区间和最值.
| π |
| 6 |
| 2π |
| 3 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若x∈[0,
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)由题意可求得A的值,
T=
-
,可得T的值,ω的值,又由题意2sin(2×
+φ)=2,可解得φ的值,即可求得解析式.
(Ⅱ)由2kπ-
≤2x+
≤2kπ+
可解得f(x)的单调增区间,若x∈[0,
]时,则可得函数f(x)的单调增区间,根据正弦函数的性质即可求得最值.
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
(Ⅱ)由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
解答:
解:(Ⅰ)∵由题意可得:A=2,
T=
-
,可得T=π,ω=
=
=2,
∵由题意可得:2sin(2×
+φ)=2
∴由五点作图法可得:φ=
∴f(x)=2sin(2x+
)
(Ⅱ)∵2kπ-
≤2x+
≤2kπ+
可解得f(x)的单调增区间是[kπ-
,kπ+
]k∈Z,
∵若x∈[0,
]时,函数f(x)的单调增区间是[0,
].
∵x∈[0,
]
∴2x+
∈[
,
]
∴当x=
时,f(x)max=2,当x=
时,f(x)min=-1.
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| T |
| 2π |
| π |
∵由题意可得:2sin(2×
| π |
| 6 |
∴由五点作图法可得:φ=
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
(Ⅱ)∵2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∵若x∈[0,
| π |
| 2 |
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴当x=
| π |
| 6 |
| π |
| 2 |
点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
当0<x<y<
时,给出以下结论(其中e是自然对数的底数):①excosy<eycosx,②excosy>eycosx,③excosx<eycosy,④excosx>eycosy,其中正确结论的序号是( )
| π |
| 4 |
| A、①③ | B、①④ | C、②③ | D、②④ |
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则( )
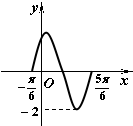

A、y=2sin(2x+
| ||
B、y=2sin(2x-
| ||
C、y=2sin(x+
| ||
D、y=-2sin(x+
|
设数列{an}为等差数列,且a2=-6,a8=6,Sn是前n项和,则( )
| A、S4<S5 |
| B、S6<S5 |
| C、S4=S5 |
| D、S6=S5 |
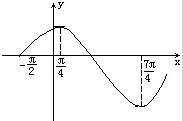 函数f(x)=sin(ωx+φ)(|φ|<
函数f(x)=sin(ωx+φ)(|φ|<