Question

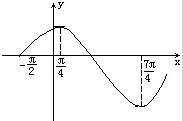函数f（x）=sin（ωx+φ）（|φ|＜

π

2

）的图象如图所示，试求：
（1）f（x）的解析式；
（2）f（x）的单调递增区间．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：（1）根据图象中所给的半个周期的长度，看出一个周期的大小，根据周期的公式做出ω的值，根据五点法，看出与第二个点对应的是

π

4

，求出φ的值即可得f（x）的解析式；
（2）由2kπ-

π

2

≤

2

3

x+

π

3

≤2kπ+

π

2

，k∈Z可解得f（x）的单调递增区间．

解答： 解：（1）∵

1

2

T=

7π

4

-

π

4

=

3π

2

，
∴T=3π
∴ω=

2π

T

=

2π

3π

=

2

3

，
∵当

2

3

x+φ=

π

2

时，x=

π

4

，
∵|φ|＜

π

2

∴φ=

π

3

，
∴f（x）=sin（

2

3

x+

π

3

）．
（2）∵由2kπ-

π

2

≤

2

3

x+

π

3

≤2kπ+

π

2

，k∈Z可解得：3kπ-

5π

4

≤x≤3kπ+

π

4

，k∈Z
∴f（x）的单调递增区间是：[3kπ-

5π

4

，3kπ+

π

4

]，k∈Z．

点评：本题考查由函数的图象确定函数的解析式，这是三角函数这一部分经常见到的一种题型，可以作为一个题目的一部分出现，也可以单独出现，其中最不好确定的一个量是φ，可以采用五点法来做出，属于基础题．