题目内容
设数列{an}为等差数列,且a2=-6,a8=6,Sn是前n项和,则( )
| A、S4<S5 |
| B、S6<S5 |
| C、S4=S5 |
| D、S6=S5 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件利用等差数列的性质求出首项和公差,由此分别求出S4,S5,S6,从而能求出结果.
解答:
解:∵数列{an}为等差数列,且a2=-6,a8=6,
∴
,解得a1=-8,d=6,
∴S4=4a1+
d=-32+36=4,
S5=5a1+
d=-40+60=20,
S6=6a1+
d=-48+90=42,
∴S4<S5.
故选:A.
∴
|
∴S4=4a1+
| 4×3 |
| 2 |
S5=5a1+
| 5×4 |
| 2 |
S6=6a1+
| 6×5 |
| 2 |
∴S4<S5.
故选:A.
点评:本题考查数列的前n项和的应用,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列两个变量之间的关系哪个不是函数关系( )
| A、人的年龄和身高 |
| B、正方形的边长和面积 |
| C、正n边形的边数与顶点角度之和 |
| D、角度与它的余弦值 |
为了调查任教班级的作业完成的情况,将班级里的52名学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知5号、31号、44号同学在样本中,那么样本中还有一位同学的编号应该是( )
| A、13 | B、17 | C、18 | D、21 |
平行于直线x+y-1=0且与圆x2+y2-2=0相切的直线的方程是( )
| A、x+y+2=0 | ||||
| B、x+y-2=0 | ||||
C、x+y+2
| ||||
| D、x+y+2=0或x+y-2=0 |
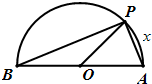 如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的( )
如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的( )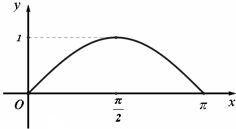



 如图:有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底是圆的直径,上底CD的端点在圆周上.梯形的周长令为y,腰长为x
如图:有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底是圆的直径,上底CD的端点在圆周上.梯形的周长令为y,腰长为x