题目内容
已知p:{x|
},q:{x|1-m≤x≤1+m,m>0}.
(1)若m=1,则p是q的什么条件?
(2)若p是q的充分不必要条件,求实数m的取值范围.
|
(1)若m=1,则p是q的什么条件?
(2)若p是q的充分不必要条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:集合,简易逻辑
分析:(1)求出不等式对应的条件,根据充分条件和必要条件的定义进行判断,
(2)根据充分条件和必要条件的定义进行判断即可.
(2)根据充分条件和必要条件的定义进行判断即可.
解答:
解 (1)因为p:{x|
}={x|-2≤x≤10},
q:{x|1-m≤x≤1+m,m>0}={x|0≤x≤2},
显然{x|0≤x≤2}?{x|-2≤x≤10},
所以p是q的必要不充分条件.
(2)由(1)知p:{x|-2≤x≤10},因为p是q的充分不必要条件,
所以
且1-m=-2与1+m=10不能同时相等,
解得m≥9,即m∈[9,+∞).
|
q:{x|1-m≤x≤1+m,m>0}={x|0≤x≤2},
显然{x|0≤x≤2}?{x|-2≤x≤10},
所以p是q的必要不充分条件.
(2)由(1)知p:{x|-2≤x≤10},因为p是q的充分不必要条件,
所以
|
解得m≥9,即m∈[9,+∞).
点评:本题主要考查充分条件和必要条件的判断和应用,根据不等式之间的关系是解决本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
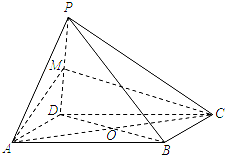 如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.
如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.