题目内容
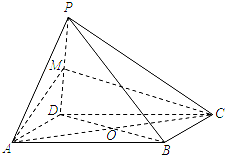 如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.
如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.(1)求证:PB∥平面AMC;
(2)求证:平面PBD⊥平面AMC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)利用三角形中位线的性质,证明OM∥PB,从而可得线面平行;
(2)先证明AC⊥平面PBD,即可证明平面PBD⊥平面AMC.
(2)先证明AC⊥平面PBD,即可证明平面PBD⊥平面AMC.
解答:
 证明:(1)连结OM,
证明:(1)连结OM,
因为O为菱形ABCD对角线的交点,
所以O为BD的中点,
又M为棱PD的中点,
所以OM∥PB,…(2分)
又OM?平面AMC,PB?平面AMC,
所以PB∥平面AMC; (6分)
(2)在菱形ABCD中,AC⊥BD,且O为AC的中点,
又MA=MC,故AC⊥OM,…(8分)
而OM∩BDO,OM,BD?平面PBD,
所以AC⊥平面PBD,…(11分)
又AC?平面AMC,
所以平面PBD⊥平面AMC. …(14分)
 证明:(1)连结OM,
证明:(1)连结OM,因为O为菱形ABCD对角线的交点,
所以O为BD的中点,
又M为棱PD的中点,
所以OM∥PB,…(2分)
又OM?平面AMC,PB?平面AMC,
所以PB∥平面AMC; (6分)
(2)在菱形ABCD中,AC⊥BD,且O为AC的中点,
又MA=MC,故AC⊥OM,…(8分)
而OM∩BDO,OM,BD?平面PBD,
所以AC⊥平面PBD,…(11分)
又AC?平面AMC,
所以平面PBD⊥平面AMC. …(14分)
点评:本小题主要考查空间线面关系等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目