题目内容
已知R上的偶函数f(x)满足对任意x∈R,f(x+2)=
,且当x∈(0,1)时,f(x)=2-x,则f(
)= .
| 1 |
| f(x) |
| 2015 |
| 2 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:由已知f(x+2)=
,将x换为x+2,求出f(x)的周期为4,结合偶函数的定义,f(
)变形到f(
),再由x∈(0,1)时,f(x)=2-x,即可得到答案.
| 1 |
| f(x) |
| 2015 |
| 2 |
| 1 |
| 2 |
解答:
解:由已知f(x+2)=
,
得,f(x+4)=
=f(x),
即函数的周期为4,
又f(x)是R上的偶函数,则f(-x)=f(x),
故f(
)=f(252×4-
)=f(-
)=f(
)
当x∈(0,1)时,f(x)=2-x,
则f(
)=2-
=
,
故f(
)═
.
故答案为:
.
| 1 |
| f(x) |
得,f(x+4)=
| 1 |
| f(x+2) |
即函数的周期为4,
又f(x)是R上的偶函数,则f(-x)=f(x),
故f(
| 2015 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x∈(0,1)时,f(x)=2-x,
则f(
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故f(
| 2015 |
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题主要考查函数的周期性和函数的奇偶性的定义及应用,是一道基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
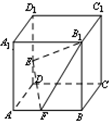 (理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是
(理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是