题目内容
已知点(1,2)是函数f(x)=ax(a>0,a≠1)的图象上一点,数列{an}的前n项和Sn=f(n)-1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| n |
| an+1 |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(I)把点(1,2)代入函数解析式中求得a,然后可得数列前n项和的表达式,进而利用an=Sn-Sn-1,求得an.
(Ⅱ)由(Ⅰ)得:bn=
,利用错位相减法,可求数列{bn}的前n项和Tn.
(Ⅱ)由(Ⅰ)得:bn=
| n |
| 2n |
解答:
解:(Ⅰ)把点(1,2)代入函数f(x)=ax,得a=2.…2分
所以Sn=f(n)-1=2n-1,
当n=1时,a1=S1=21-1=1;…3分
当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1
经验证可知n=1时,也适合上式,
∴an=2n-1.…6分
(Ⅱ)由(Ⅰ)得:bn=
,
,
两式相减可得
Tn=
+
+…+
-n
=1-(1+
)•(
)n,
所以Tn=2-
.…12分.
所以Sn=f(n)-1=2n-1,
当n=1时,a1=S1=21-1=1;…3分
当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1
经验证可知n=1时,也适合上式,
∴an=2n-1.…6分
(Ⅱ)由(Ⅰ)得:bn=
| n |
| 2n |
|
两式相减可得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| n |
| 2 |
| 1 |
| 2 |
所以Tn=2-
| n+2 |
| 2n |
点评:熟练掌握当n=1时,a1=S1=1;当n≥2时,an=Sn-Sn-1求an、等差数列和等比数列的前n项和公式是解题的关键.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,试判断BD1与平面AEC的位置关系,并说明理由.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,试判断BD1与平面AEC的位置关系,并说明理由.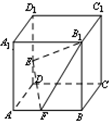 (理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是
(理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是