题目内容
若f(x)=x2+2(a-1)x+2在(-∞,4)上是减函数,求a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:首先求出对称轴方程,进一步利用二次函数的对称轴与单调区间的关系确定结果.
解答:
解:函数f(x)=x2+2(a-1)x+2
对称轴方程为:x=1-a
由于x在(-∞,4)上是减函数.
1-a≥4
所以解得:a≤-3
故答案为:a≤-3
对称轴方程为:x=1-a
由于x在(-∞,4)上是减函数.
1-a≥4
所以解得:a≤-3
故答案为:a≤-3
点评:本题考查的知识要点:二次函数的对称轴与单调区间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于函数f(x)=2(sinx-cosx)cosx的四个结论:
P1:最大值为
;
P2:最小正周期为π;
P3:单调递增区间为[kπ-
,kπ+
π],k∈Z;
P4:函数y=f(x)的一条对称轴是x=
其中正确的有( )
P1:最大值为
| 2 |
P2:最小正周期为π;
P3:单调递增区间为[kπ-
| π |
| 8 |
| 3 |
| 8 |
P4:函数y=f(x)的一条对称轴是x=
| 7π |
| 8 |
其中正确的有( )
| A、1 个 | B、2个 |
| C、3个 | D、4个 |
若loga
<1,则a的取值范围是( )
| 1 |
| 3 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
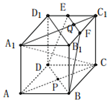 如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、
如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、