题目内容
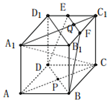 如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、
如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、A1C1与EF的交点.
(1)求证:D、B、F、E四点共面;
(2)若A1C与面DBFE交于点R,求证:P、Q、R三点共线.
考点:棱柱的结构特征
专题:证明题,空间位置关系与距离
分析:(1)由BB1
DD1可得BD
B1D1,又由E、F分别为D1C1和B1C1的中点,可得EF
B1D1,从而得证;
(2)由题意可得平面AC1∩平面BE=PQ,再由A1C与面DBFE交于点R,可得R∈平面AC1,R∈平面BE,从而可得R∈PQ.
|
|
|
| 1 |
| 2 |
(2)由题意可得平面AC1∩平面BE=PQ,再由A1C与面DBFE交于点R,可得R∈平面AC1,R∈平面BE,从而可得R∈PQ.
解答:
证明:(1)∵正方体ABCD-A1B1C1D1中,BB1
DD1,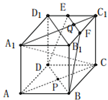
∴BD
B1D1,
又∵E、F分别为D1C1和B1C1的中点,
EF
B1D1,
∴EF
BD,
∴D、B、F、E四点共面.
(2)∵Q∈平面AC1,Q∈平面BE,P∈平面AC1,P∈平面BE,
∴平面AC1∩平面BE=PQ,
又∵A1C与面DBFE交于点R,
∴R∈平面AC1,R∈平面BE,
∴R∈PQ,
即P、Q、R三点共线.
|

∴BD
|
又∵E、F分别为D1C1和B1C1的中点,
EF
|
| 1 |
| 2 |
∴EF
|
| 1 |
| 2 |
∴D、B、F、E四点共面.
(2)∵Q∈平面AC1,Q∈平面BE,P∈平面AC1,P∈平面BE,
∴平面AC1∩平面BE=PQ,
又∵A1C与面DBFE交于点R,
∴R∈平面AC1,R∈平面BE,
∴R∈PQ,
即P、Q、R三点共线.
点评:本题考查了学生的识图能力及平行性的证明与应用,同时考查了三点共线的证明方法,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
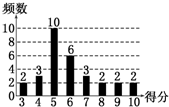 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为. |
| x |
A、me=m0=
| ||
B、me=m0<
| ||
C、me<m0<
| ||
D、m0<me<
|
已知定义在R上的函数f(x),g(x)满足
=ax,且f′(x)g(x)>f(x)g′(x),
+
=
.若有穷数列{
}的前n项和为Sn,则满足不等式Sn>2015的最小正整数n等于( )
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| A、7 | B、8 | C、9 | D、10 |
如图是一个几何体的三视图,则该几何体的体积是( )
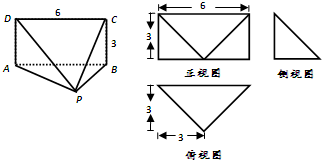

| A、54 | B、27 | C、18 | D、9 |
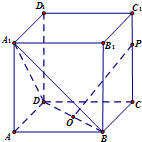 (理)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
(理)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|