题目内容
已知函数f(x)=x+
.
(Ⅰ)判断f(x)的奇偶性,并证明你的结论;
(Ⅱ)若a>0,证明:函数f(x)在[
,+∞)内是增函数.
| a |
| x |
(Ⅰ)判断f(x)的奇偶性,并证明你的结论;
(Ⅱ)若a>0,证明:函数f(x)在[
| a |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(Ⅰ)根据函数奇偶的定义即可判断f(x)的奇偶性;
(Ⅱ)根据函数单调性的定义即可证明:函数f(x)在[
,+∞)内是增函数.
(Ⅱ)根据函数单调性的定义即可证明:函数f(x)在[
| a |
解答:
解:(Ⅰ)函数f(x)的定义域为{x|x≠0},则f(-x)=-x-
=-(x+
)=-f(x).
故函数f(x)是奇函数;
(Ⅱ)设x2>x1>
,则f(x2)-f(x1)=x2+
-x1-
=(x2-x1)•
∵x2>x1>
,∴x2-x1>0,x2x1>a,
∴x2x1-a>0,
则f(x2)-f(x1)>0,即f(x2)>f(x1),
即函数f(x)在[
,+∞)内是增函数.
| a |
| x |
| a |
| x |
故函数f(x)是奇函数;
(Ⅱ)设x2>x1>
| a |
| a |
| x2 |
| a |
| x1 |
| x1x2-a |
| x1x2 |
∵x2>x1>
| a |
∴x2x1-a>0,
则f(x2)-f(x1)>0,即f(x2)>f(x1),
即函数f(x)在[
| a |
点评:本题主要考查函数奇偶性和单调性的判断和证明,根据相应的定义是解决本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
在z轴上与点A(-4,1,7)和点B(3,5,-2)等距离的点C的坐标为( )
| A、(0,0,1) | ||
| B、(0,0,2) | ||
C、(0,0,
| ||
D、(0,0,
|
已知O,T,P在△ABC所在平面内,且
+
+
=
,|
|=|
|=|
|,且
•
=
•
=
•
,则点O,T,P依次是△ABC的( )
| OA |
| OB |
| OC |
| 0 |
| TA |
| TB |
| TC |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| A、外心 重心 垂心 |
| B、重心 外心 内心 |
| C、重心 外心 垂心 |
| D、外心 重心 内心 |
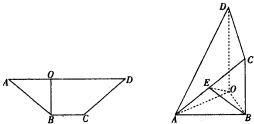 在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.
在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.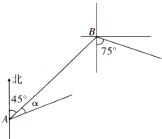 在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)
在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)