题目内容
已知抛物线D:y2=2px(p>0)的焦点为F,P是抛物线上一动点,Q是圆M:(x+1)2+(y-2)2=
上一动点,且|PF|+|PQ|最小值为
.
(1)求抛物线D的方程;
(2)已知动直线l过点N(4,0),交抛物线D与A,B两点,坐标原点O为线段NG中点,求证:∠AGN=∠BGN.
| 1 |
| 2 |
3
| ||
| 2 |
(1)求抛物线D的方程;
(2)已知动直线l过点N(4,0),交抛物线D与A,B两点,坐标原点O为线段NG中点,求证:∠AGN=∠BGN.
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)确定圆心坐标为M(-1,2),半径为
,将|PF|+|PQ|最小值为
,转化为|PF|+|PM|最小值为2
,即|FM|=2
,利用两点间距离公式,求出p,就可以求出抛物线D的方程.
(2)设A(x1,y1),B(x2,y2),由于O为NG之中点,故当l⊥x轴时,由抛物线的对称性知,一定有:∠AGN=∠BGN,当l不垂直x轴时,设l:y=k(x-4),代入抛物线方程得k2x2-4(2k2+1)x+16k2=0,由此能够证明:∠AGN=∠BGN.
| ||
| 2 |
3
| ||
| 2 |
| 2 |
| 2 |
(2)设A(x1,y1),B(x2,y2),由于O为NG之中点,故当l⊥x轴时,由抛物线的对称性知,一定有:∠AGN=∠BGN,当l不垂直x轴时,设l:y=k(x-4),代入抛物线方程得k2x2-4(2k2+1)x+16k2=0,由此能够证明:∠AGN=∠BGN.
解答:
解:(1)圆M:(x+1)2+(y-2)2=
的圆心坐标为M(-1,2),半径为
,
∵|PF|+|PQ|最小值为
,Q是圆M:(x+1)2+(y-2)2=
上一动点,
∴当Q、P、F三点共线时,|QF|最小,M、Q、P、F四点共线时,|MF|最小为2
,
∴
=2
,
∴p=2,
∴抛物线D的方程是y2=4x;
(2)设A(x1,y1),B(x2,y2),
由于O为NG之中点,故当l⊥x轴时,由抛物线的对称性知,一定有:∠AGN=∠BGN,
当l不垂直x轴时,设l:y=k(x-4),
代入抛物线方程得k2x2-4(2k2+1)x+16k2=0,
∴x1+x2=
,x1x2=16,
∴kAG+kBG=
+
=0,
∴∠AGN=∠BGN.
| 1 |
| 2 |
| ||
| 2 |
∵|PF|+|PQ|最小值为
3
| ||
| 2 |
| 1 |
| 2 |
∴当Q、P、F三点共线时,|QF|最小,M、Q、P、F四点共线时,|MF|最小为2
| 2 |
∴
(
|
| 2 |
∴p=2,
∴抛物线D的方程是y2=4x;
(2)设A(x1,y1),B(x2,y2),
由于O为NG之中点,故当l⊥x轴时,由抛物线的对称性知,一定有:∠AGN=∠BGN,
当l不垂直x轴时,设l:y=k(x-4),
代入抛物线方程得k2x2-4(2k2+1)x+16k2=0,
∴x1+x2=
| 4(2k2+1) |
| k2 |
∴kAG+kBG=
| k(x1-4) |
| x1+4 |
| k(x2-4) |
| x2+4 |
∴∠AGN=∠BGN.
点评:本题考查抛物线方程的求法,直线和抛物线的位置关系,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.

练习册系列答案
相关题目
在半径不等的两个圆内,1弧度的圆心角( )
| A、所对弧长相等 |
| B、所对的弦长相等 |
| C、所对弦长等于各自半径 |
| D、所对的弧长等于各自半径 |
设向量
=(2,3),
=(-1,2),若m
+
与
-2
平行,则实数m等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|

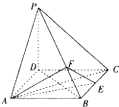 如图,ABCD是正方形,PD⊥平面ABCD,点E是BC中点,点F在PB上,且PE=2FB.
如图,ABCD是正方形,PD⊥平面ABCD,点E是BC中点,点F在PB上,且PE=2FB.