题目内容
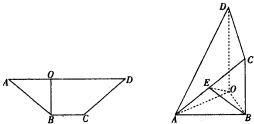 在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.
在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.(Ⅰ)求证:OE⊥CD;
(Ⅱ)若梯形ABCD的面积是4,求C-BOE的体积VC-BOE;
(Ⅲ)求二面角E-OB-A的大小.
考点:二面角的平面角及求法,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由题意得OA⊥OB,平面AOB⊥平面OBCD,从而AO⊥平面OBCD,进而AO⊥CD,又CD⊥OC,由此能证明OE⊥CD.
(Ⅱ)设BC=x,由梯形ABCD的面积是4,知
=4,由AO⊥平面OBCD,能求出E到平面OBCD的距离,由此能求出三棱C-BOE的体积VC-BOE.
(Ⅲ)取AB中点F,过F作FG⊥OB于G,连接EF,EG,由已知得∠EGF为二面角E-OB-A的平面角,由此能求出二面角E-OB-A的大小.
(Ⅱ)设BC=x,由梯形ABCD的面积是4,知
| (x+3x)x |
| 2 |
(Ⅲ)取AB中点F,过F作FG⊥OB于G,连接EF,EG,由已知得∠EGF为二面角E-OB-A的平面角,由此能求出二面角E-OB-A的大小.
解答:
(Ⅰ)证明:由题意得OA⊥OB,平面AOB⊥平面OBCD,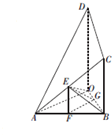
∴AO⊥平面OBCD,
∵CD⊆平面OBCD,∴AO⊥CD,
又∵AD=3BC=3BO,
∴OD=
OC=
CD,
∴CD⊥OC,
∵AO∩OC=O,∴CD⊥平面AOC,
又OE⊆平面AOC,∴OE⊥CD.
(Ⅱ)解:设BC=x,由梯形ABCD的面积是4,知
=4,
∴BC=OB=OA=
,
由(Ⅰ)知AO⊥平面OBCD,又E是AC中点,
∴E到平面OBCD的距离h=
=
,
∴VC-BOE=VR-BOC=
×
×
×
×
=
.
(Ⅲ)解:如图所示,取AB中点F,过F作FG⊥OB于G,
连接EF,EG,
∴EF∥BC∥OD,
∴EF⊥平面AOB,又OB⊆平面AOB,
∴OB⊥EF,∴OB⊥平面EFG,
又EG⊆平面EFG,∴OB⊥FG,
∴∠EGF为二面角E-OB-A的平面角,
∵AD=3BC=3BO,
设BC=1,
在Rt△EGF中,EF=FG=
,
∴tan∠EGF=
=1,∴∠EGF=
,
∴二面角E-OB-A的大小为
.

∴AO⊥平面OBCD,
∵CD⊆平面OBCD,∴AO⊥CD,
又∵AD=3BC=3BO,
∴OD=
| 2 |
| 2 |
∴CD⊥OC,
∵AO∩OC=O,∴CD⊥平面AOC,
又OE⊆平面AOC,∴OE⊥CD.
(Ⅱ)解:设BC=x,由梯形ABCD的面积是4,知
| (x+3x)x |
| 2 |
∴BC=OB=OA=
| 2 |
由(Ⅰ)知AO⊥平面OBCD,又E是AC中点,
∴E到平面OBCD的距离h=
| OA |
| 2 |
| ||
| 2 |
∴VC-BOE=VR-BOC=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 6 |
(Ⅲ)解:如图所示,取AB中点F,过F作FG⊥OB于G,
连接EF,EG,
∴EF∥BC∥OD,
∴EF⊥平面AOB,又OB⊆平面AOB,
∴OB⊥EF,∴OB⊥平面EFG,
又EG⊆平面EFG,∴OB⊥FG,
∴∠EGF为二面角E-OB-A的平面角,
∵AD=3BC=3BO,
设BC=1,
在Rt△EGF中,EF=FG=
| 1 |
| 2 |
∴tan∠EGF=
| EF |
| FG |
| π |
| 4 |
∴二面角E-OB-A的大小为
| π |
| 4 |
点评:本题考查异面直线垂直的证明,考查三棱锥的体积的求法,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若如图的框图所给的程序运行结果为S=20,那么判断框中应填入的关于k的条件是( )

| A、k=9 | B、k≤8 |
| C、k<8 | D、k>8 |