题目内容
在△ABC中,a,b,c分别为内角A,B,C所对的边,b=c,且满足
=
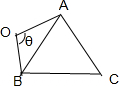
.若点O是△ABC外一点,∠AOB=θ(0<θ<π),OA=2OB=2,平面四边形OACB面积的最大值是( )
| sinB |
| sinA |
| 1-cosB |
| cosA |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
考点:正弦定理
专题:解三角形
分析:依题意,可求得△ABC为等边三角形,利用三角形的面积公式与余弦定理可求得SOACB=2sin(θ-
)+
(0<θ<π),从而可求得平面四边形OACB面积的最大值.
| π |
| 3 |
5
| ||
| 4 |
解答:
 解:△ABC中,∵b=c,
解:△ABC中,∵b=c,
=
,∴sinBcosA+cosBsinA=sinA,即sin(A+B)=sin(π-C)=sinC=sinA,
∴A=C,又b=c,∴△ABC为等边三角形.
∴SOACB=S△AOB+S△ABC
=
•OA•OB•sinθ+
•AB2•sin
=
×2×1×sinθ+
(OA2+OB2-2OA•OB•cosθ)
=sinθ-
cosθ+
=2sin(θ-
)+
.
∵0<θ<π,∴-
<θ-
<
,故当θ-
=
时,sin(θ-
)取得最大值为1,
故SOACB=的最大值为2+
=
,
故选:A.
 解:△ABC中,∵b=c,
解:△ABC中,∵b=c,| sinB |
| sinA |
| 1-cosB |
| cosA |
∴A=C,又b=c,∴△ABC为等边三角形.
∴SOACB=S△AOB+S△ABC
=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
=sinθ-
| 3 |
5
| ||
| 4 |
| π |
| 3 |
5
| ||
| 4 |
∵0<θ<π,∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
故SOACB=的最大值为2+
5
| ||
| 4 |
8+5
| ||
| 4 |
故选:A.
点评:题考查三角函数中的恒等变换应用,考查余弦定理的应用,求得SOACB=2sin(θ-
)+
是解题的关键,也是难点,考查等价转化思想与运算求解能力,属于中档题.
| π |
| 3 |
5
| ||
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
实数x,y满足x2+y2-4x+1=0,则
的最大值为( )
| y+x |
| x |
A、1+
| ||
B、2+
| ||
C、1+
| ||
D、2+
|
将自然数1,2,3,…,n,…按第k组含k个数的规则分组:(1),(2,3),(4,5,6),…那么2012所在的组是( )
| A、第64组 | B、第63组 |
| C、第62组 | D、第61组 |
在等差数列{an}中,2a3+a9=3,则数列{an}的前9项和等于( )
| A、9 | B、6 | C、3 | D、12 |