题目内容
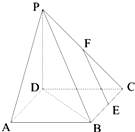 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.(1)求证:EF∥平面PBD;
(2)如果AB=PD,求EF与平面ABCD所成角的正切值.
考点:直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)先证明出EF∥BP,进而根据线面平行的判定定理证明出EF∥平面PBD.
(2)先证明出∠PBD为直线EF与平面ABCD所成的角,进而在Rt△PBD中求得tan∠PBD的值.
(2)先证明出∠PBD为直线EF与平面ABCD所成的角,进而在Rt△PBD中求得tan∠PBD的值.
解答:
(1)证明:在△PBC中,E,F为BC和PC的中点,
∴EF∥BP,
∵EF?平面PBD,PB?平面PBD,
∴EF∥平面PBD.
(2)∵EF∥BP,PD⊥平面ABCD,
∴∠PBD即为直线EF与平面ABCD所成的角,
∵ABCD为正方形,BD=
AB,
∴在Rt△PBD中,tan∠PBD=
=
.
∴EF与平面ABCD所成角的正切值为
.
∴EF∥BP,
∵EF?平面PBD,PB?平面PBD,
∴EF∥平面PBD.
(2)∵EF∥BP,PD⊥平面ABCD,
∴∠PBD即为直线EF与平面ABCD所成的角,
∵ABCD为正方形,BD=
| 2 |
∴在Rt△PBD中,tan∠PBD=
| PD |
| BD |
| ||
| 2 |
∴EF与平面ABCD所成角的正切值为
| ||
| 2 |
点评:本题主要考查了线面平行的判定定理的应用,直线与平面所成的角.考查了学生对立体几何知识的综合运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
已知集合M={x|-1<x-a<2},N={x|x2≥x},若M∪N=R,则实数a的取值范围是( )
| A、(-1,1) |
| B、[-1,1) |
| C、[-1,1] |
| D、(-1,1] |
已知复数z=
+
(m∈R)的实部是虚部的2倍,则m等于( )
| 1+mi |
| 4-3i |
| m |
| 25 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
随机变量ξ服从正态分布N(0,σ2),且P(-2<ξ≤2)=0.6,则P(ξ>2)等于( )
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
 某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告:
某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告: