题目内容
设命题p:函数f(x)=x3-ax-1在区间[-1,1]上单调递减;命题q:函数y=x2+ax+1的最小值不大于0.如果命题p或q为真命题,p且q为假命题,求实数a的取值范围是多少.
考点:复合命题的真假
专题:简易逻辑
分析:根据题意可知p,q为一真一假,通过导函数先求出p,q为真时a的取值范围,再分类讨论一真一假时,p,q的交集即可求解.
解答:
解:p为真命题?f′(x)=3x2-a≤0在[-1,1]上恒成立?a≥3x2在[-1,1]上恒成立?a≥3.
q为真命题?△=a2-4≥0恒成立?a≤-2或a≥2.
由题意p和q有且只有一个是真命题.
p真q假?
⇒a∈∅
p假q真?
⇒a≤-2或2≤a<3.
综上所述:a∈(-∞,-2]∪[2,3).
q为真命题?△=a2-4≥0恒成立?a≤-2或a≥2.
由题意p和q有且只有一个是真命题.
p真q假?
|
⇒a∈∅
p假q真?
|
⇒a≤-2或2≤a<3.
综上所述:a∈(-∞,-2]∪[2,3).
点评:涉及到单调性问题和最值问题一般用求导的方法来解决.对于这种涉及到两个命题的并、交的复合命题,要充分讨论,把各种情况考虑进去,最后通过求交集或者并集来求解

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
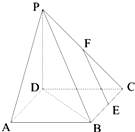 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点. (1)已知角a的终边经过点P(3,-4)求:
(1)已知角a的终边经过点P(3,-4)求: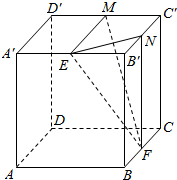 在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.
在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.