题目内容
已知sinα、cosα是方程4x2+2
x+m=0的两实根,求:
(1)m的值;
(2)cos3(
-α)+cos3α的值.
| 6 |
(1)m的值;
(2)cos3(
| π |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)根据题意利用韦达定理表示出sinα+cosα=-
,sinαcosα=
,利用同角三角函数间基本关系化简即可求出m的值;
(2)原式利用诱导公式化简后,再利用立方和公式变形,将各自的值代入计算即可求出值.
| ||
| 2 |
| m |
| 4 |
(2)原式利用诱导公式化简后,再利用立方和公式变形,将各自的值代入计算即可求出值.
解答:
解:(1)∵sinα、cosα是方程4x2+2
x+m=0的两实根,
∴sinα+cosα=-
,sinαcosα=
,
∵sin2α+cos2α=1,即(sinα+cosα)2-2sinαcosα=1,
∴
-
=1,
解得:m=1;
(2)∵m=1,
∴sinα+cosα=-
,sinαcosα=
,
则cos3(
-α)+cos3α=sin3α+cos3α=(sinα+cosα)(sin2α+cos2α-sinαcosα)=-
×(1-
)=-
.
| 6 |
∴sinα+cosα=-
| ||
| 2 |
| m |
| 4 |
∵sin2α+cos2α=1,即(sinα+cosα)2-2sinαcosα=1,
∴
| 3 |
| 2 |
| m |
| 2 |
解得:m=1;
(2)∵m=1,
∴sinα+cosα=-
| ||
| 2 |
| 1 |
| 4 |
则cos3(
| π |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
3
| ||
| 8 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知三棱锥的底面是边长为2正三角形,侧面均为等腰直角三角形,则此三棱锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a>b,m>0,则下列不等式中,恒成立的是( )
| A、(a+m)2>(b+m)2 | ||||
B、
| ||||
| C、(a-m)3>(b-m)3 | ||||
| D、|am|>|bm| |
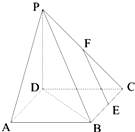 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.