题目内容
已知命题p:函数y=logm(6-mx)在[1,2]上单调递减.
(1)求实数m的取值范围;
(2)命题q:方程x2-2x+m+1=0在(0,+∞)内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
(1)求实数m的取值范围;
(2)命题q:方程x2-2x+m+1=0在(0,+∞)内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
考点:复合命题的真假
专题:函数的性质及应用,简易逻辑
分析:(1)因为m>0,则y=6-mx是增函数,而整个函数是减函数,所以底数0<m<1,再结合定义域,即在[1,2]上函数有意义,得到关于m的不等式组,解之即可;
(2)先把q为真时的m范围求出,结合二次函数的图象可知,只需f(0)≤0或△=0即可,然后根据“p或q为真,p且q为假”可得,两命题一真一假,然后分两种情况列出不等式组求解.
(2)先把q为真时的m范围求出,结合二次函数的图象可知,只需f(0)≤0或△=0即可,然后根据“p或q为真,p且q为假”可得,两命题一真一假,然后分两种情况列出不等式组求解.
解答:
解:(1)由题意,m>0,∴y=6-mx在[1,2]上是减函数,且满足6-2×m>0,∴0<m<3,
又∵函数y=logm(6-mx)在[1,2]上单调递减,根据复合函数单调性的判断方法,应有m>1,
∴若p为真,则1<m<3.
(2)令f(x)=x2-2x+m+1,该函数对称轴为x=1,
①当△=4-4(m+1)=0时,m=0,f(x)=0的根为1,符合题意;
②当△>0即m<0时,结合图象只需f(0)=m+1≤0,解得m≤-1,
综上,若q为真,则m≤-1或m=0;
∵“p或q为真,p且q为假”,命题p、q一真一假,
可得
或
,
解得m≤-1或m=0或1<m<3,
∴m的取值范围是(-∞,-1]∪{0}∪(1,3).
又∵函数y=logm(6-mx)在[1,2]上单调递减,根据复合函数单调性的判断方法,应有m>1,
∴若p为真,则1<m<3.
(2)令f(x)=x2-2x+m+1,该函数对称轴为x=1,
①当△=4-4(m+1)=0时,m=0,f(x)=0的根为1,符合题意;
②当△>0即m<0时,结合图象只需f(0)=m+1≤0,解得m≤-1,
综上,若q为真,则m≤-1或m=0;
∵“p或q为真,p且q为假”,命题p、q一真一假,
可得
|
|
解得m≤-1或m=0或1<m<3,
∴m的取值范围是(-∞,-1]∪{0}∪(1,3).
点评:本题考查了:复合函数单调性的判断方法,及“同增异减”;一元二次方程根的分布问题,一般利用二次函数的图象来分析解决.同时准确记忆“或”“且”“非”命题真假的判断方法是最终解决问题的关键.

练习册系列答案
相关题目
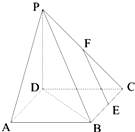 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点. (1)已知角a的终边经过点P(3,-4)求:
(1)已知角a的终边经过点P(3,-4)求: